题目内容
在△ABC中，角A=30°，B=60°，则b：c=（ ）
| A、1：2 | ||
| B、2：3 | ||
C、1：
| ||
D、
|
考点：正弦定理
专题：计算题,解三角形
分析：先求出角C，然后由正弦定理得b：c=sinB：sinC，代入数值可求．
解答：
解：∵A=30°，B=60°，
∴C=180°-30°-60°=90°，
由正弦定理，得b：c=sinB：sinC=sin60°：sin90°=
：2，
故选：D．
∴C=180°-30°-60°=90°，
由正弦定理，得b：c=sinB：sinC=sin60°：sin90°=
| 3 |
故选：D．
点评：该题考查正弦定理及其应用，属基础题，准确记忆定理内容并熟练应用是解题关键．
练习册系列答案
应用题作业本系列答案
相关题目
函数y=ax+1-2（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny+1=0上，其中m、n＞0，则
+
的最小值为（ ）
| 1 |
| m |
| 2 |
| n |
| A、3 | ||
B、3+2
| ||
C、2+2
| ||
D、2
|
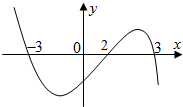若连续函数f（x）在R上可导，其导函数为f′（x），且函数y=（2-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）| A、f（x）有极大值f（3）和极小值f（2） |
| B、f（x）有极大值f（-3）和极小值f（2） |
| C、f（x）有极大值f（3）和极小值f（-3） |
| D、f（x）有极大值f（-3）和极小值f（3） |
在等比数列{an}中，若a1=3，a2=9，则数列{an}的前4项和为（ ）
| A、81 | B、120 |
| C、168 | D、192 |
已知非零向量
，
且|
|=|
|，则a与b的关系是（ ）
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
=
，则tanα的值是（ ）
| sinα-cosα |
| 2sinα+3cosα |
| 1 |
| 5 |
A、±
| ||
B、
| ||
C、-
| ||
| D、无法确定 |