题目内容
已知F1，F2分别为双曲线
-
=1（a＞0，b＞0）的左、右焦点，O为原点，A为右顶点，P为双曲线左支上的任意一点，若
存在最小值为12a，则双曲线离心率e的取值范围是 （ ）
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1|-|OA| |
| A、[5，+∞） |
| B、（2，5] |
| C、（1，5] |
| D、（1，2） |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题意，
=2|PF2|，根据
存在最小值为12a，可得a，c的关系，即可求出双曲线离心率e的取值范围．
| |PF2|2 |
| |PF1|-|OA| |
| |PF2|2 |
| |PF1|-|OA| |
解答：
解：由题意，
=2|PF2|．
∵
存在最小值为12a，
∴2（c+a）≤12a，
∴e≤5，
∵e＞1，
∴1＜e≤5．
故选：C．
| |PF2|2 |
| |PF1|-|OA| |
∵
| |PF2|2 |
| |PF1|-|OA| |
∴2（c+a）≤12a，
∴e≤5，
∵e＞1，
∴1＜e≤5．
故选：C．
点评：本题考查双曲线的简单性质，考查双曲线的定义，比较基础．
练习册系列答案
相关题目
已知f（x）=2xlnx，g（x）=-x2+ax-3，对一切x∈（0，+∞），f（x）≥g（x）恒成立，则实数a的取值范围是（ ）
| A、（-∞，4] |
| B、（-∞，5] |
| C、[6，+∞） |
| D、[4，+∞） |
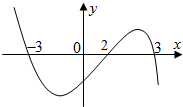若连续函数f（x）在R上可导，其导函数为f′（x），且函数y=（2-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）| A、f（x）有极大值f（3）和极小值f（2） |
| B、f（x）有极大值f（-3）和极小值f（2） |
| C、f（x）有极大值f（3）和极小值f（-3） |
| D、f（x）有极大值f（-3）和极小值f（3） |
设集合A={1，2，3，5，7}，集合B={2，4，5，6，8}，则集合A∩B=（ ）
| A、{1，3，5，7} |
| B、{2，5} |
| C、{2，6，8} |
| D、{1，2，3，4，5，6，7，8} |
在等比数列{an}中，若a1=3，a2=9，则数列{an}的前4项和为（ ）
| A、81 | B、120 |
| C、168 | D、192 |
已知非零向量
，
且|
|=|
|，则a与b的关系是（ ）
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
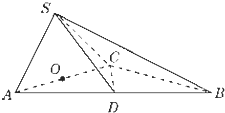已知三棱锥S-ABC中，平面ASC⊥平面ABC，O、D分别为AC、AB的中点，AS=CS=CD=AD=