题目内容
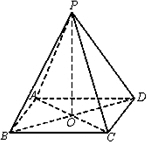如图，在四棱锥P-ABCD中，底面ABCD是矩形，四条侧棱长均相等且BD交AC于点O．（1）求证：AB∥平面PCD；
（2）求证：PO⊥平面ABCD．
考点：直线与平面平行的判定,直线与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：（1）由矩形ABCD，对边平行得到AB∥CD，结合线面平行的判定定理得到AB∥平面PCD；
（2）在矩形ABCD中，点O为AC，BD的中点，可得PO⊥AC，PO⊥BD，进而由线面垂直的判定定理得到PO⊥平面ABCD．
（2）在矩形ABCD中，点O为AC，BD的中点，可得PO⊥AC，PO⊥BD，进而由线面垂直的判定定理得到PO⊥平面ABCD．
解答：
证明：（1）在矩形ABCD中，AB∥CD，又AB?平面PCD，CD?平面PCD，
所以AB∥平面PCD…（7分）
（2）在矩形ABCD中，点O为AC，BD的中点，
因为PA=PB=PC=PD，
所以PO⊥AC，PO⊥BD，
因为AC∩BD=O，AC，BD?平面ABCD，
所以PO⊥平面ABCD，…（14分）
所以AB∥平面PCD…（7分）
（2）在矩形ABCD中，点O为AC，BD的中点，
因为PA=PB=PC=PD，
所以PO⊥AC，PO⊥BD，
因为AC∩BD=O，AC，BD?平面ABCD，
所以PO⊥平面ABCD，…（14分）
点评：本题考查直线与平面垂直的判定，直线与平面平行的判定，考查空间想象能力，属于中档题．
练习册系列答案
相关题目
参数方程
（θ为参数）表示的曲线是（ ）
|
| A、圆 | B、直线 | C、线段 | D、射线 |
设集合A={1，2，3，5，7}，集合B={2，4，5，6，8}，则集合A∩B=（ ）
| A、{1，3，5，7} |
| B、{2，5} |
| C、{2，6，8} |
| D、{1，2，3，4，5，6，7，8} |
已知非零向量
，
且|
|=|
|，则a与b的关系是（ ）
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设f（x）=
，则不等式f（x）≥2的解集为（ ）
|
| A、（-∞，1]∪[3，+∞） |
| B、（-∞，-1]∪[2，+∞） |
| C、[3，+∞） |
| D、（-∞，-1] |