题目内容
设集合M={x|-2≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示以集合y=c(
)mt(c,m为常数)为定义域,N为值域的函数关系的是( )
| 1 |
| 2 |
A、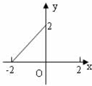 |
B、 |
C、 |
D、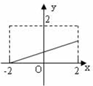 |
考点:函数的图象
专题:函数的性质及应用
分析:分析已知中四个图象,利用定义域为{x|-2≤x≤2},可以排除A答案,根据函数的概念,可以排除C答案,根据值域为{y|0≤y≤2},可以排除D答案,进而得到答案
解答:
解:选项A中的函数定义域为{x|-2≤x≤0},值域为{y|0≤y≤2},不满足题意中对定义域的要求,故A不正确;
选项B函数定义域为{x|-2≤x≤2},值域为{y|0≤y≤2},满足题意要求,故B正确;
选项C中y轴与图象有两个交点,不满足函数概念中,有唯一的值与自变量对应,故C不正确;
选项D中函数定义域为{x|-2≤x≤2},值域为{y|0≤y≤1},不满足题意中对值域的要求,故D不正确;
故选:B
选项B函数定义域为{x|-2≤x≤2},值域为{y|0≤y≤2},满足题意要求,故B正确;
选项C中y轴与图象有两个交点,不满足函数概念中,有唯一的值与自变量对应,故C不正确;
选项D中函数定义域为{x|-2≤x≤2},值域为{y|0≤y≤1},不满足题意中对值域的要求,故D不正确;
故选:B
点评:本题考查的知识点是函数的图象与图象变化,其中熟练掌握函数的概念及根据函数图象分析函数三要素及性质的方法是解答本题的关键.

练习册系列答案
相关题目
五位同学参加某作家的签字售书活动,则甲、乙都排在丙前面的方法有( )
| A、20种 | B、24种 |
| C、40种 | D、56种 |
已知两条直线l1:x+y-2=0,l2:3x+ay+2=0,且l1⊥l2,则a=( )
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
设a>1,定义f(n)=
+
+…+
,如果对任意的n∈N*且n≥2,不等式12f(n)+7logab>7+7loga+1b恒成立,则实数b的取值范围是( )
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
A、(2,
| ||
| B、(0,1) | ||
| C、(0,4) | ||
| D、(1,+∞) |
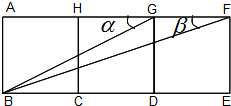 如图,有三个并排放在一起的正方形,∠AGB=α,∠AFB=β.
如图,有三个并排放在一起的正方形,∠AGB=α,∠AFB=β.