Question

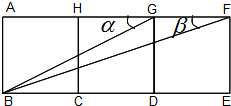如图，有三个并排放在一起的正方形，∠AGB=α，∠AFB=β．
（1）求α+β的度数；
（2）求函数y=sin²x+

3

sinxcosx-1的最大值及取得最大值时候的x值．

Answer 1

考点：两角和与差的正切函数

专题：三角函数的求值

分析：（1）不妨设正方形边长为1，易知tanα=

1

2

，tanβ=

1

3

，由两角和的正切公式可得tan（α+β）=1，由角的范围可得；
（2）化简可得y=sin（2x-

π

6

）-

1

2

，由正弦函数的最值可得．

解答： 解：（1）不妨设正方形边长为1，易知tanα=

1

2

，tanβ=

1

3

，
∴tan（α+β）=

tanα+tanβ

1-tanαtanβ

=

1 2 + 1 3

1- 1 2 × 1 3

=1，
又∵α和β均为锐角，∴0＜α+β＜π，
∴α+β=

π

4

（2）化简可得y=

1-cos2x

2

+

3

2

sin2x-1
=

3

2

sin2x-

1

2

cos2x-

1

2

=sin（2x-

π

6

）-

1

2

∴当2x-

π

6

=2kπ+

π

2

即x=kπ+

π

3

（k∈Z）时，函数y的最大值为

1

2

点评：本题考查两角和与差的三角函数，涉及三角函数的最值，属基础题．