题目内容
在平面直角坐标系中,已知点(6,8),将线段OP绕着点O逆时针旋转
后得到线段OQ,则Q的坐标为 .
| 3π |
| 4 |
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:由条件根据两个复数乘积的几何意义,求得
对应的复数为(6+8i)•(cos
+isin
)的值,可得Q的坐标.
| OQ |
| 3π |
| 4 |
| 3π |
| 4 |
解答:
解:有题义可得,
对应的复数为(6+8i)•(cos
+isin
)=(6+8i)(-
+
i)=-7
-
i,
故
的坐标为(-7
,-
),即Q的坐标为(-7
,-
),
故答案为:(-7
,-
).
| OQ |
| 3π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
故
| OQ |
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:(-7
| 2 |
| 2 |
点评:本题主要考查两个复数乘积的几何意义,两个向量坐标形式的运算,属于基础题.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,若g(x)=f(x+1)+5,g(x)=f(x+1)+5,g′(x)为g(x)的导函数,对?x∈R,总有g′(x)>2x,则g(x)<x2+4的解集为( )
| A、(-∞,-1) |
| B、(-∞,1) |
| C、R |
| D、(-1,+∞) |


 某市新年第一个月前10天监测到空气污染指数如表(主要污染物为可吸入颗粒物):(第天监测得到的数据记为ai)
某市新年第一个月前10天监测到空气污染指数如表(主要污染物为可吸入颗粒物):(第天监测得到的数据记为ai)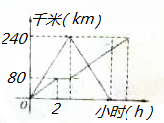 甲,乙两车在连通A,B,C三地的公路上行驶,甲车从A地出发匀速向C地行驶,中途到达B地并在B地停留1小时后按原速驶向C地;同时乙车从C地出发匀速向A地行驶,到达A地后,立即按原路原速返回到C地并停留.在两车行驶的过程中,甲,乙两车距各自出发地的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,请结合图象回答下列问题:
甲,乙两车在连通A,B,C三地的公路上行驶,甲车从A地出发匀速向C地行驶,中途到达B地并在B地停留1小时后按原速驶向C地;同时乙车从C地出发匀速向A地行驶,到达A地后,立即按原路原速返回到C地并停留.在两车行驶的过程中,甲,乙两车距各自出发地的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,请结合图象回答下列问题: