题目内容
9.设集合M={x|y=$\sqrt{{{log}_2}x-1}$},N={x||x-1|≤2},则M∩N=( )| A. | [2,+∞) | B. | [-1,3] | C. | [2,3] | D. | [-1,2] |
分析 通过求解绝对值不等式和对数不等式化简集合M与集合N,然后直接利用交集运算求解.
解答 解:∵log2x-1≥0,即log2x≥1=log22,
∴x≥2,
∴M=[2,+∞),
∵|x-1|≤2,
∴-1≤x≤3,
∴N=[-1,3],
则M∩N=[2,3],
故选:C.
点评 本题考查了交集及其运算,考查了绝对值不等式和对数不等式的解法,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
20.若集合A={-2,-1,0,1,2},B={x|2x>1},则A∩B=( )
| A. | {-1,2} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
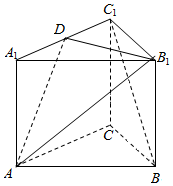 已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.
已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.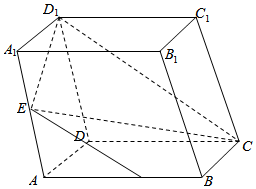
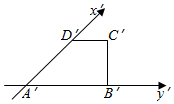 如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.
如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.