题目内容
18.计算:lg20-lg2-${(\frac{1}{3})^{{{log}_3}2}}$=$\frac{1}{2}$.分析 直接利用导数的运算法则化简求解即可.
解答 解:lg20-lg2-${(\frac{1}{3})^{{{log}_3}2}}$=lg10-${3}^{lo{g}_{3}{2}^{-1}}$=1-$\frac{1}{2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查对数运算法则的应用,考查计算能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.设集合M={x|y=$\sqrt{{{log}_2}x-1}$},N={x||x-1|≤2},则M∩N=( )
| A. | [2,+∞) | B. | [-1,3] | C. | [2,3] | D. | [-1,2] |
6.复数($\frac{1+i}{1-i}$)3的模是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
7.为了研究钟表与三角函数的关系,以9点与3点所在直线为x轴,以6点与12点为y轴,设秒针针尖指向位置P(x,y),若初始位置为P0($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),秒针从P0(注此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t(秒)的函数关系为( )
| A. | y=sin($\frac{π}{30}$t+$\frac{π}{3}$) | B. | y=sin($\frac{π}{30}$t-$\frac{π}{3}$) | C. | y=sin(-$\frac{π}{30}$t+$\frac{π}{3}$) | D. | y=sin(-$\frac{π}{30}$t-$\frac{π}{3}$) |
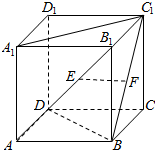 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB1,BC1的中点,则以下结论中不成立的是③.(填序号)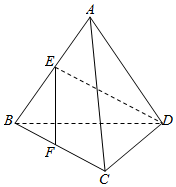 如图,已知正三角形BCD外一点A满足AB=AD,E,F分别是AB,BC的中点,且EF⊥DE,则∠BAC=$\frac{π}{2}$.
如图,已知正三角形BCD外一点A满足AB=AD,E,F分别是AB,BC的中点,且EF⊥DE,则∠BAC=$\frac{π}{2}$.