题目内容
1．如图，在正方体ABCD-A1B1C1D1中．E是AA1的中点，画出过D1，C，E的平面与平面ABB1A1的交线，并说明理由．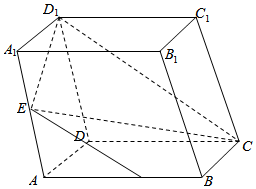
分析 取AB中点F，连结EF、CF，则EF是过D1，C，E的平面与平面ABB1A1的交线．
解答 
解：取AB中点F，连结EF、CF，则EF是过D1，C，E的平面与平面ABB1A1的交线
理由如下：连结A1B，在△A1AB中，
∵E、F分别是AA1、AB的中点，
∴EF∥A1B，
∵在正方体ABCD-A1B1C1D1中，A1B∥D1C，
∴D1C∥EF，∴平面D1EFC是D1，C，E的平面，
∵平面D1EFC∩平面ABB1A1=EF，
∴EF是过D1，C，E的平面与平面ABB1A1的交线．
点评 本题考查两平面的交线的画法，是中档题，解题时要认真审题，注意平面的基本性质及推论的合理运用．
练习册系列答案
天天向上口算本系列答案
相关题目
11．方程$\frac{x^2}{2+m}+\frac{y^2}{m+1}$=1表示双曲线，则m的取值范围是（ ）
| A． | （-2，-1） | B． | （-2，+∞） | C． | （-∞，-1） | D． | （-∞，-2）∪（-1，+∞） |
12．若一个边长为a的正三角形，以其中一条高作为轴旋转，则所得旋转体的表面积为（ ）
| A． | $\frac{1}{4}$πa2 | B． | $\frac{1}{2}$πa2 | C． | $\frac{3}{4}$πa2 | D． | $\frac{1}{8}$πa2 |
9．设集合M={x|y=$\sqrt{{{log}_2}x-1}$}，N={x||x-1|≤2}，则M∩N=（ ）
| A． | [2，+∞） | B． | [-1，3] | C． | [2，3] | D． | [-1，2] |
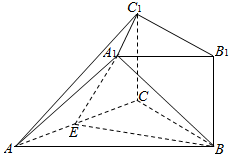在如图所示的几何体中，四边形BB1C1C是矩形，BB1⊥平面ABC，A1B1∥AB，AB=2A1B1，E是AC的中点．
6．复数（$\frac{1+i}{1-i}$）3的模是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
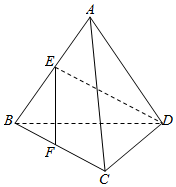如图，已知正三角形BCD外一点A满足AB=AD，E，F分别是AB，BC的中点，且EF⊥DE，则∠BAC=$\frac{π}{2}$．
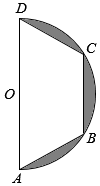如图，等腰梯形ABCD，BC=$\frac{1}{2}$AD，将直径为4的半圆内的阴影部分以直径AD所在直线为轴，旋转一周得到一几何体，求该几何体的体积．