题目内容
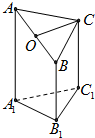 如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.
如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)求AB与平面AA1C1C所成的角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:计算题,作图题,证明题,空间位置关系与距离
分析:(1)作OD∥AA1交A1B1于D,连C1D,说明ODC1C是平行四边形,从而证明OC∥平面A1B1C1;
(2)过B作截面BA2C2∥面A1B1C1,分别交AA1,CC1于A2,C2,作BH⊥A2C2于H,连结AH,说明∠BAH就是AB与面AA1C1C所成的角.从而求正弦值.
(2)过B作截面BA2C2∥面A1B1C1,分别交AA1,CC1于A2,C2,作BH⊥A2C2于H,连结AH,说明∠BAH就是AB与面AA1C1C所成的角.从而求正弦值.
解答:
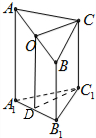 解:(1)证明:如图,作OD∥AA1交A1B1于D,连C1D.
解:(1)证明:如图,作OD∥AA1交A1B1于D,连C1D.
则OD∥BB1∥CC1,
∵O是AB的中点,
∴OD=
(AA1+BB1)=3=CC1,
∴ODC1C是平行四边形,
∴OC∥C1D,
又∵C1D?平面C1B1A1,且OC?平面C1B1A1;
∴OC∥面A1B1C1.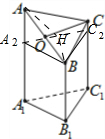
(2)解:如图,过B作截面BA2C2∥面A1B1C1,分别交AA1,CC1于A2,C2,作BH⊥A2C2于H,
∵平面A2BC2⊥平面AA1C1C,
∴BH⊥面AA1C1C.连结AH,
则∠BAH就是AB与面AA1C1C所成的角.
∵BH=
,AB=
,
∴sin∠BAH=
=
.
 解:(1)证明:如图,作OD∥AA1交A1B1于D,连C1D.
解:(1)证明:如图,作OD∥AA1交A1B1于D,连C1D.则OD∥BB1∥CC1,
∵O是AB的中点,
∴OD=
| 1 |
| 2 |
∴ODC1C是平行四边形,
∴OC∥C1D,
又∵C1D?平面C1B1A1,且OC?平面C1B1A1;
∴OC∥面A1B1C1.

(2)解:如图,过B作截面BA2C2∥面A1B1C1,分别交AA1,CC1于A2,C2,作BH⊥A2C2于H,
∵平面A2BC2⊥平面AA1C1C,
∴BH⊥面AA1C1C.连结AH,
则∠BAH就是AB与面AA1C1C所成的角.
∵BH=
| ||
| 2 |
| 5 |
∴sin∠BAH=
| BH |
| AB |
| ||
| 10 |
点评:本题考查了学生的空间想象力及作图能力,作出恰当的辅助线是解决本题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数y=sin2x+m•cosx+
m-
在闭区间[0,
]上的最大值是1,则满足条件的m值为( )
| 5 |
| 8 |
| 3 |
| 2 |
| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
以下说法正确的是( )
| A、若直线a不平行于平面α,则直线a与平面α相交 |
| B、直线a和b是异面直线,若直线c∥a,则c与b一定相交 |
| C、若直线a和b都和平面α平行,则a和b也平行 |
| D、若直线c平行直线a,直线b⊥a,则b⊥c |
 在长方形ABCD中,AB=3,BC=1,E为DC的三等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的摄影恰好落在边AB上,则当F运动时,二面角D-AF-B平面角余弦值的变化范围是
在长方形ABCD中,AB=3,BC=1,E为DC的三等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的摄影恰好落在边AB上,则当F运动时,二面角D-AF-B平面角余弦值的变化范围是 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,E、F分别是PB、CD的中点,且PB=PC=PD=4.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,E、F分别是PB、CD的中点,且PB=PC=PD=4.