题目内容
已知函数f(x)=x2+mx+m+1(m>5)的两个零点分别为tanα,tanβ,且α,β∈(-
,
),则α+β= .
| π |
| 2 |
| π |
| 2 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:利用韦达定理结合两角和的正切函数以及诱导公式求出tanα,tanβ的值.然后利用两角和的正切函数求出tan(α+β)的值,即可求出结果.
解答:
解:由f(x)=x2+mx+m+1(m>5)的两个零点分别为tanα,tanβ,
已知方程x2+mx+m+1=0(a>1)的两根分别为tanα,tanβ,
得:
,
∴tan(α+β)=
=
=1.
∵m>5,
∴tanα+tanβ=-m<0,
∵α,β∈(-
,
),∴α+β∈(-π,0),
∴α+β=-
,
故答案为:-
.
已知方程x2+mx+m+1=0(a>1)的两根分别为tanα,tanβ,
得:
|
∴tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
| -m |
| 1-m-1 |
∵m>5,
∴tanα+tanβ=-m<0,
∵α,β∈(-
| π |
| 2 |
| π |
| 2 |
∴α+β=-
| 3π |
| 4 |
故答案为:-
| 3π |
| 4 |
点评:本题考查两角和的正切公式、韦达定理的应用,考查计算能力与转化思想,注意角的范围的求解,这是易错点.

练习册系列答案
相关题目
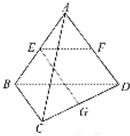 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算: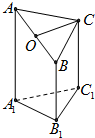 如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.
如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.