题目内容
若函数y=sin2x+m•cosx+
m-
在闭区间[0,
]上的最大值是1,则满足条件的m值为( )
| 5 |
| 8 |
| 3 |
| 2 |
| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:三角函数的最值
专题:常规题型,三角函数的图像与性质
分析:利用平方关系式把sin2x化成1-cos2x,把函数看作关于cosx的二次函数问题来解决.
解答:
解:y=sin2x+m•cosx+
m-
=1-cos2x+mcosx+
m-
∵x∈[0,
],∴0≤cosx≤1
y=-(cosx-
)2+
+
-
①当
≤0,即m≤0时,
ymax=
-
=1,得m=
(舍);
②当0<
≤1,即0<m≤2时,
ymax=
+
-
=1,得a=-4(舍)或a=
;
③当
>1,即m>2时,
ymax=m+
m-
=1,得m=
(舍).
∴m=
.
故选D.
| 5 |
| 8 |
| 3 |
| 2 |
=1-cos2x+mcosx+
| 5 |
| 8 |
| 3 |
| 2 |
∵x∈[0,
| π |
| 2 |
y=-(cosx-
| m |
| 2 |
| m2 |
| 4 |
| 5m |
| 8 |
| 1 |
| 2 |
①当
| m |
| 2 |
ymax=
| 5m |
| 8 |
| 1 |
| 2 |
| 12 |
| 5 |
②当0<
| m |
| 2 |
ymax=
| m2 |
| 4 |
| 5m |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
③当
| m |
| 2 |
ymax=m+
| 5 |
| 8 |
| 3 |
| 2 |
| 20 |
| 13 |
∴m=
| 3 |
| 2 |
故选D.
点评:解决本题的关键是把三角函数的最值问题转化为二次函数的最值问题解决,要特别注意定义域及分类的方法.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
把红、黄、蓝3张卡片随机分给甲、乙、丙三人,每人1张,事件A:“甲得红卡”与事件B:“乙得红卡”是( )
| A、不可能事件 |
| B、必然事件 |
| C、对立事件 |
| D、互斥且不对立事件 |
不等式1≤|x|<2的解集为( )
| A、[1,2 ) |
| B、(-2,-1] |
| C、[1,2)∪(-2,-1] |
| D、(1,2]∪[-2,-1) |
函数f(x)=
的定义域为( )
log
|
| A、(3,+∞) |
| B、[3,+∞) |
| C、(3,4] |
| D、(-∞,4] |
正方形ABCD沿对角线AC折成直二面角,则异面直线AD和BC所成角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
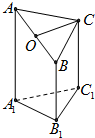 如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.
如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.