题目内容
已知点O为锐角△ABC的外心，AB=6，AC=10，
=x
+y
，2x+10y=5，则△ABC的外接圆半径为（ ）
| AO |
| AB |
| AC |
| A、3 | ||
B、3
| ||
| C、6 | ||
D、6
|
考点：向量在几何中的应用
专题：平面向量及应用
分析：首先，设A（0，0），C（10，0），B（6cosθ，6sinθ），然后，结合O点横坐标为5，建立关系式，求解B（2，4
），从而得到|BC|，然后，再借助于正弦定理确定其外接圆的半径．
| 2 |
解答：
解：设A（0，0），C（10，0），B（6cosθ，6sinθ）
又O点横坐标为5，
∵
=x
+y
，
∴5=x6cosθ+y*10=2x+10y，
∴cosθ=
；即cos∠BAC=
，
∴sin∠BAC=
，
∴B（2，4
），
∴|BC|=
=
=4
，
设该三角形的外接圆的半径为R，
则根据正弦定理，得
=
=6
，
∴2R=6
，
∴R=3
．
故选：B．
又O点横坐标为5，
∵
| AO |
| AB |
| AC |
∴5=x6cosθ+y*10=2x+10y，
∴cosθ=
| 1 |
| 3 |
| 1 |
| 3 |
∴sin∠BAC=
2
| ||
| 3 |
∴B（2，4
| 2 |
∴|BC|=
(10-2)2+(0-4
|
| 96 |
=4
| 6 |
设该三角形的外接圆的半径为R，
则根据正弦定理，得
| BC |
| sin∠BAC |
4
| ||||
|
| 3 |
∴2R=6
| 3 |
∴R=3
| 3 |
故选：B．
点评：本题重点考查了平面向量的直角坐标运算，坐标运算性质、三角形的外接圆、正弦定理等知识，属于中档题，解题关键是准确设出三角形的三个顶点的坐标，然后，正确利用正弦定理进行确定其外接圆的半径．
练习册系列答案
相关题目
不等式1≤|x|＜2的解集为（ ）
| A、[1，2 ） |
| B、（-2，-1] |
| C、[1，2）∪（-2，-1] |
| D、（1，2]∪[-2，-1） |
正方形ABCD沿对角线AC折成直二面角，则异面直线AD和BC所成角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
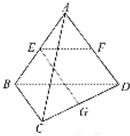如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：
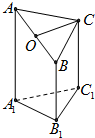如图是一个正三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=1，AA1=4，BB1=2，CC1=3．