题目内容
 在长方形ABCD中,AB=3,BC=1,E为DC的三等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的摄影恰好落在边AB上,则当F运动时,二面角D-AF-B平面角余弦值的变化范围是
在长方形ABCD中,AB=3,BC=1,E为DC的三等分点(靠近C处),F为线段EC上一动点(包括端点),现将△AFD沿AF折起,使D点在平面内的摄影恰好落在边AB上,则当F运动时,二面角D-AF-B平面角余弦值的变化范围是考点:二面角的平面角及求法
专题:计算题,作图题,空间位置关系与距离
分析:过点D作DM⊥AF于点O,交AB于点M,不妨设二面角D-AF-B的平面解为θ,则cosθ=
=
=
,从而求其取值范围.
| OM |
| OD |
| OA |
| OF |
| 1 |
| x2 |
解答:
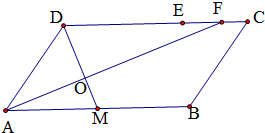 解:如图,过点D作DM⊥AF于点O,交AB于点M,不妨设二面角D-AF-B的平面解为θ,
解:如图,过点D作DM⊥AF于点O,交AB于点M,不妨设二面角D-AF-B的平面解为θ,
则cosθ=
,
设DF=x,2≤x≤3,由勾股定理,
OD=
,OF=
,OA=
,∴cosθ=
=
=
在[2,3]上是减函数,
∴
≤cosθ≤
.
故答案为:[
,
].
 解:如图,过点D作DM⊥AF于点O,交AB于点M,不妨设二面角D-AF-B的平面解为θ,
解:如图,过点D作DM⊥AF于点O,交AB于点M,不妨设二面角D-AF-B的平面解为θ,则cosθ=
| OM |
| OD |
设DF=x,2≤x≤3,由勾股定理,
OD=
| x | ||
|
|
|
| OM |
| OD |
| OA |
| OF |
| 1 |
| x2 |
∴
| 1 |
| 9 |
| 1 |
| 4 |
故答案为:[
| 1 |
| 9 |
| 1 |
| 4 |
点评:本题考查了学生的作图能力及空间想象力,注意折起前后的等量关系是本题解决的关键,属于中档题.

练习册系列答案
相关题目
函数f(x)=
的定义域为( )
log
|
| A、(3,+∞) |
| B、[3,+∞) |
| C、(3,4] |
| D、(-∞,4] |
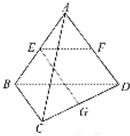 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:(1)
| EF |
| BA |
(2)
| EF |
| DC |
(3)EG的长;
(4)异面直线AG与CE所成角的余弦值.
设全集U=R,集合A={x|
≥0},B={x|1<2x<8},则(∁UA)∩B等于( )
| x+1 |
| x-2 |
| A、[-1,3) |
| B、(0,2] |
| C、(1,2] |
| D、(2,3) |
函数f(x)=(4-x)ex的单调递减区间是( )
| A、(-∞,4) |
| B、(-∞,3) |
| C、(4,+∞) |
| D、(3,+∞) |
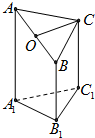 如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.
如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.