题目内容
若关于x的方程4x-a•2x+4=0有实数解，则实数a的取值范围是 ．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：可分离出a，转化为函数f（x）=
的值域问题，令2x=t，利用基本不等式和不等式的性质求值域即可．
| -4x-4 |
| 2x |
解答：
解：a=
，令2x=t（t＞0），则
=-
，
因为t+
≥4，所以
≤-4，
所以a的范围为（-∞，-4]，
故答案为：（-∞，-4]．
| -4x-4 |
| 2x |
| -4x-4 |
| 2x |
| t2+4 |
| t |
因为t+
| 4 |
| t |
| -4x-4 |
| 2x |
所以a的范围为（-∞，-4]，
故答案为：（-∞，-4]．
点评：本题考查方程有解问题、基本不等式求最值问题，同时考查转化思想和换元法．
练习册系列答案
期末集结号系列答案
相关题目
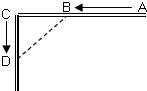如图，快艇和轮船分别从A地和C地同时开出，航行路线互相垂直，快艇的速度为40千米/时，轮船的速度是15千米/时，A、C两地间的距离是120千米．问经过多少时间．快艇和轮船之间的距离最小？（精确到0.1小时）
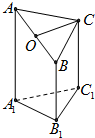如图是一个正三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=1，AA1=4，BB1=2，CC1=3．若函数f（x）=
x3+x2+mx是R上的单调函数，则实数m的取值范围是（ ）
| 1 |
| 3 |
| A、（1，+∞） |
| B、（-∞，1） |
| C、[1，+∞） |
| D、（-∞，1] |