题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,E、F分别是PB、CD的中点,且PB=PC=PD=4.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,E、F分别是PB、CD的中点,且PB=PC=PD=4.(1)求证:PA⊥平面ABCD;
(2)求证:EF∥平面PAD;
(3)求二面角A-PB-C的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)取BC的中点M,连结AM,PM,由已知条件推导出PA⊥BC,PA⊥CD,由此能证明PA⊥平面ABCD.
(2)取PA的中点N,连结EN,ND,由已知得四边形ENDF是平行四边形,由此能证明EF∥平面PAD.
(3)取AB的中点G,过G作GH⊥PB于点H,连结HC,GC,由已知得∠GHC是二面角A-PB-C的平面角,由此能求出二面角A-PB-C的余弦值.
(2)取PA的中点N,连结EN,ND,由已知得四边形ENDF是平行四边形,由此能证明EF∥平面PAD.
(3)取AB的中点G,过G作GH⊥PB于点H,连结HC,GC,由已知得∠GHC是二面角A-PB-C的平面角,由此能求出二面角A-PB-C的余弦值.
解答:
 (1)证明:取BC的中点M,连结AM,PM.
(1)证明:取BC的中点M,连结AM,PM.
∵AB=BC,∠ABC=60°,∴△ABC为正三角形,∴AM⊥BC.
又PB=PC,∴PM⊥BC,AM∩PM=M,
∴BC⊥平面PAM,PA?平面PAM,∴PA⊥BC,
同理可证PA⊥CD,
又BC∩CD=C,∴PA⊥平面ABCD.…(4分).
(2)证明:取PA的中点N,连结EN,ND.
∵PE=EB,PN=NA,∴EN∥AB,且EN=
AB.
又FD∥AB,且FD=
AB,∴EN
DF,
∴四边形ENDF是平行四边形,
∴EF∥ND,而EF?平面PAD,ND?平面PAD,
∴EF∥平面PAD.…(8分)
(3)解:取AB的中点G,过G作GH⊥PB于点H,连结HC,GC.
则CG⊥AB,又CG⊥PA,PA∩AB=A,
∴CG⊥平面PAB.∴HC⊥PB,
∴∠GHC是二面角A-PB-C的平面角.
在Rt△PAB中,AB=2,PB=4,∴PA=2
.
又Rt△BHG∽Rt△BAP,∴
=
,∴HG=
.
在Rt△HGC中,可求得GC=
,
∴HC=
,∴cos∠GHC=
,
故二面角A-PB-C的余弦值为
.…(12分).
 (1)证明:取BC的中点M,连结AM,PM.
(1)证明:取BC的中点M,连结AM,PM.∵AB=BC,∠ABC=60°,∴△ABC为正三角形,∴AM⊥BC.
又PB=PC,∴PM⊥BC,AM∩PM=M,
∴BC⊥平面PAM,PA?平面PAM,∴PA⊥BC,
同理可证PA⊥CD,
又BC∩CD=C,∴PA⊥平面ABCD.…(4分).
(2)证明:取PA的中点N,连结EN,ND.
∵PE=EB,PN=NA,∴EN∥AB,且EN=
| 1 |
| 2 |
又FD∥AB,且FD=
| 1 |
| 2 |
| ||
. |
∴四边形ENDF是平行四边形,
∴EF∥ND,而EF?平面PAD,ND?平面PAD,
∴EF∥平面PAD.…(8分)
(3)解:取AB的中点G,过G作GH⊥PB于点H,连结HC,GC.
则CG⊥AB,又CG⊥PA,PA∩AB=A,
∴CG⊥平面PAB.∴HC⊥PB,
∴∠GHC是二面角A-PB-C的平面角.
在Rt△PAB中,AB=2,PB=4,∴PA=2
| 3 |
又Rt△BHG∽Rt△BAP,∴
| HG |
| PA |
| BG |
| PB |
| ||
| 2 |
在Rt△HGC中,可求得GC=
| 3 |
∴HC=
| ||
| 2 |
| ||
| 5 |
故二面角A-PB-C的余弦值为
| ||
| 5 |
点评:本题考查PA⊥平面ABCD的证明,考查EF∥平面PAD的证明,考查二面角A-PB-C的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
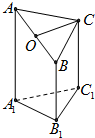 如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.
如图是一个正三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=1,AA1=4,BB1=2,CC1=3.