题目内容
14.函数f(x)=log2(4x+1)的值域为( )| A. | [0,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (1,+∞) |
分析 由指数函数的值域可得4x+1>1,再由对数函数的单调性和值域可得.
解答 解:∵4x+1>1,∴log2(4x+1)>log21=0,
∴函数的值域为(0,+∞),
故选:B.
点评 本题考查指数函数和对数函数的值域,属基础题.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
9.若cos2x=$\frac{1}{2}$,其中$\frac{π}{2}$<x<π,则x的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{3}$ |
6.已知a>b>m>0,则( )
| A. | $sin\frac{b-m}{a-m}<sin\frac{b+m}{a+m}<sin\frac{b}{a}$ | B. | $sin\frac{b-m}{a-m}>sin\frac{b+m}{a+m}>sin\frac{b}{a}$ | ||
| C. | $sin\frac{b-m}{a-m}>sin\frac{b}{a}>sin\frac{b+m}{a+m}$ | D. | $sin\frac{b-m}{a-m}<sin\frac{b}{a}<sin\frac{b+m}{a+m}$ |
3.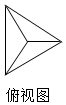 一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )
一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )
 一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )
一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\sqrt{3}$ |
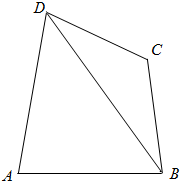 如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求
如图,平面四边形ABCD中,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,求