题目内容
3.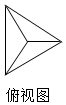 一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )
一个正四面体的体积为$\frac{2\sqrt{2}}{3}$,它的三视图中的俯视图如图所示(其中三个小三角形全等),侧视图是一个三角形,则这个三角形的面积是( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\sqrt{3}$ |
分析 由已知正四面体的体积求得棱锥的棱长,再根据俯视图判断几何体的放置位置,从而可得侧视图是等腰三角形,求出底边上的高,计算三角形的面积即可.
解答 解:设正四面体的棱长为a,则体积V=$\frac{1}{3}$×$\frac{1}{2}$×a2×$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{6}}{3}$a=$\frac{2\sqrt{2}}{3}$,
∴a=2,
根据正四面体的俯视图可得,其左视图为等腰三角形,
底边为侧棱长2,且底边上的高为四面体的高$\frac{\sqrt{6}}{3}$×2=$\frac{2\sqrt{6}}{3}$;
∴侧视图的面积为S=$\frac{1}{2}$×2×$\frac{2\sqrt{6}}{3}$=$\frac{2\sqrt{6}}{3}$.
故选:B.
点评 本题考查了由俯视图的位置求几何体的侧视图面积,根据俯视图的放置位置判断左视图的结构特征是解答本题的关键.

练习册系列答案
相关题目
13.设复数z满足(1+i)z=2,则z的共轭复数$\overline{z}$=( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
14.函数f(x)=log2(4x+1)的值域为( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (1,+∞) |
18.若命题:“?x∈R,x2-2ax+a≤0”为假命题,则$\frac{{2{a^2}+1}}{a}$的最小值是( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
15.设i为虚数单位,则i2014=( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
12.随机变量X的分布列如下:
其中a,b,c成等差数列,则P(|x|=1)=( )
| X | -1 | 0 | 1 |
| P | a | b | c |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
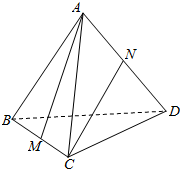 在正四面体(四个面都是正三角形的四面体是正四面体)中,M,N分别是BC和AD的中点,试作出异面直线AM与CN所成角.
在正四面体(四个面都是正三角形的四面体是正四面体)中,M,N分别是BC和AD的中点,试作出异面直线AM与CN所成角.