题目内容
4.若sinα=$\frac{3}{5}$,求cos($α+\frac{π}{3}$)的值.分析 先由同角三角函数关系式求出cosα,再由三角函数加法定理能求出结果.
解答 解:∵sinα=$\frac{3}{5}$,∴cosα=$±\sqrt{1-(\frac{3}{5})^{2}}$=$±\frac{4}{5}$,
当cosα=-$\frac{4}{5}$时,cos($α+\frac{π}{3}$)=cosαcos$\frac{π}{3}$-sin$αsin\frac{π}{3}$=-$\frac{4}{5}$×$\frac{1}{2}$-$\frac{3}{5}$×$\frac{\sqrt{3}}{2}$=-$\frac{4+3\sqrt{3}}{10}$.
当cosα=$\frac{4}{5}$时,cos($α+\frac{π}{3}$)=cosαcos$\frac{π}{3}$-sin$αsin\frac{π}{3}$=$\frac{4}{5}$×$\frac{1}{2}$-$\frac{3}{5}$×$\frac{\sqrt{3}}{2}$=$\frac{4-3\sqrt{3}}{10}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意同角三角函数关系式和三角函数加法定理的合理运用.

练习册系列答案
相关题目
14.函数f(x)=log2(4x+1)的值域为( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (1,+∞) |
15.设i为虚数单位,则i2014=( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
12.随机变量X的分布列如下:
其中a,b,c成等差数列,则P(|x|=1)=( )
| X | -1 | 0 | 1 |
| P | a | b | c |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
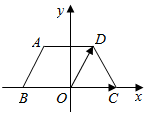 如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.
如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.