题目内容
19．在△ABC中，B=45°，b=8，则$\frac{a+b+c}{sinA+sinB+sinC}$=8$\sqrt{2}$．分析 根据题意，由正弦定理可得$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{8}{sin45°}$=8$\sqrt{2}$，进而可得a=8$\sqrt{2}$sinA，b=8$\sqrt{2}$sinB，c=8$\sqrt{2}$sinC，将其代入$\frac{a+b+c}{sinA+sinB+sinC}$计算可得答案．
解答 解：在△ABC中，根据题意，由正弦定理可得：$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{8}{sin45°}$=8$\sqrt{2}$，
则a=8$\sqrt{2}$sinA，b=8$\sqrt{2}$sinB，c=8$\sqrt{2}$sinC，
而$\frac{a+b+c}{sinA+sinB+sinC}$=$\frac{8\sqrt{2}（sinA+sinB+sinC）}{sinA+sinB+sinC}$=8$\sqrt{2}$，
故答案为：8$\sqrt{2}$．
点评 本题考查正弦定理的运用，涉及分式的运算，熟悉并掌握正弦定理的内容是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
9．函数$y=sin（2x-\frac{π}{3}）$与$y=cos（2x+\frac{2π}{3}）$的图象关于直线x=a对称，则a可能是（ ）
| A． | $\frac{π}{24}$ | B． | $\frac{π}{12}$ | C． | $\frac{π}{8}$ | D． | $\frac{11π}{24}$ |
10．在复平面内，复数$\frac{2+i}{2i}$对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
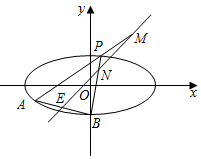如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1，（a＞b＞0），点B是其下顶点，直线x+3y+6=0与椭圆C交于A，B两点（点A在x轴下方），且线段AB的中点E在直线y=x上．
14．函数f（x）=log2（4x+1）的值域为（ ）
| A． | [0，+∞） | B． | （0，+∞） | C． | [1，+∞） | D． | （1，+∞） |
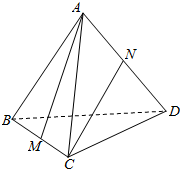在正四面体（四个面都是正三角形的四面体是正四面体）中，M，N分别是BC和AD的中点，试作出异面直线AM与CN所成角．
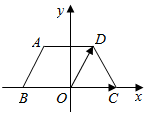如图，在直角坐标平面内，等腰梯形ABCD的下底BC在x轴上，BC的中点是坐标原点0，已知AD=AB=DC=1，BC=2．