题目内容
2.在△ABC中,角A,B,C的对边分别为a,b,c.(1)若b=3,c=1,A=60°,求a;
(2)若a=30,b=10$\sqrt{3}$,A=60°,求B,C,c.
分析 (1)使用余弦定理解出;
(2)使用正弦定理解出.
解答 解:(1)由余弦定理得a2=b2+c2-2bccosA=9+1-2×$3×1×\frac{1}{2}$=7,
∴a=$\sqrt{7}$.
(2)由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,即$\frac{30}{\frac{\sqrt{3}}{2}}=\frac{10\sqrt{3}}{sinB}$,解得sinB=$\frac{1}{2}$,
∴B=150°(舍)或B=30°.
∴C=180°-A-B=90°.
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=20$\sqrt{3}$.
点评 本题考查了正余弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
13.设复数z满足(1+i)z=2,则z的共轭复数$\overline{z}$=( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
10.在复平面内,复数$\frac{2+i}{2i}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.函数f(x)=log2(4x+1)的值域为( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (1,+∞) |
12.随机变量X的分布列如下:
其中a,b,c成等差数列,则P(|x|=1)=( )
| X | -1 | 0 | 1 |
| P | a | b | c |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
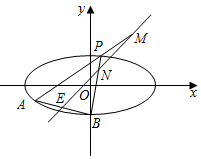 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),点B是其下顶点,直线x+3y+6=0与椭圆C交于A,B两点(点A在x轴下方),且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),点B是其下顶点,直线x+3y+6=0与椭圆C交于A,B两点(点A在x轴下方),且线段AB的中点E在直线y=x上.