题目内容
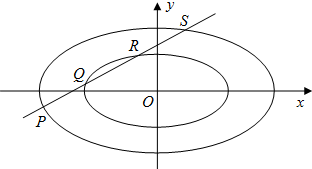（理）已知中心在原点O，左焦点为F1（-1，0）的椭圆C1的左顶点为A，上顶点为B，F1到直线AB的距离为
| ||
| 7 |
（1）求椭圆C1的方程；
（2）过点P（3，0）作直线l，使其交椭圆C1于R、S两点，交直线x=1于Q点．问：是否存在这样的直线l，使|PQ|是|PR|、|PS|的等比中项？若存在，求出直线l的方程；若不存在，说明理由．
（3）若椭圆C1方程为：
| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| m2 |
| y2 |
| n2 |
| PS |
| RS |
| QS |
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）确定直线AB方程，利用F1到直线AB的距离为
|OB|，结合b2=a2-1，求出椭圆的几何量，即可求椭圆C1的方程；
（2）分类讨论，设直线l方程为：x=my+3，代人椭圆C1的方程，利用|PQ|是|PR|、|PS|的等比中项，结合韦达定理，即可求出直线l的方程；
（3）求出椭圆C1的3倍相似椭圆C2的方程，将y=kx+b分别代人椭圆C1、C2方程，利用韦达定理，结合
+
=2
，即可求出动点E（k，b）的轨迹方程．
| ||
| 7 |
（2）分类讨论，设直线l方程为：x=my+3，代人椭圆C1的方程，利用|PQ|是|PR|、|PS|的等比中项，结合韦达定理，即可求出直线l的方程；
（3）求出椭圆C1的3倍相似椭圆C2的方程，将y=kx+b分别代人椭圆C1、C2方程，利用韦达定理，结合
| PS |
| RS |
| QS |
解答：
解：（1）设椭圆C1方程为：
+
=1（a＞b＞0），
∴直线AB方程为：
+
=1…1分
∴F1（-1，0）到直线AB距离为d=
=
b，
∴a2+b2=7（a-1）2…2分
又b2=a2-1，解得：a=2，b=
…3分
故：椭圆C1方程为：
+
=1．…4分
（2）当直线l与x轴重合时，|PQ|=2，而|PR|•|PS|=1×5=5，∴|PQ|2≠|PR|•|PS|
若存在直线l，使|PQ|是|PR|、|PS|的等比中项，
则可设直线l方程为：x=my+3…5分
代人椭圆C1的方程，得：3（my+3）2+4y2=12，即：（3m2+4）y2+18my+15=0
∴△=（18m）2-4×15（3m2+4）=48（3m2-5）
记R（x1，y1），S（x2，y2），Q（x0，y0），
∴y1y2=
，y0=-
…7分
∵|PQ|2=|PR|•|PS|，即
=
⇒
=
，
∴y1y2=
∴
=
，解得：m2=
，符合△＞0，
∴m=±
…9分
故存在直线l，使|PQ|是|PR|、|PS|的等比中项，其方程为x=±
y+3，即：y=±
(x-3)…10分
（3）椭圆C1的3倍相似椭圆C2的方程为：
+
=1…11分
设Q、R、P、S各点坐标依次为（x1，y1）、（x2，y2）、（x3，y3）、（x4，y4）
将y=kx+b代人椭圆C1方程，得：（3+4k2）x2+8kbx+4b2-12=0
∴△1=(8kb)2-4(3+4k2)(4b2-12)=48(4k2+3-b2)＞0（*）
此时：x1+x2=-
，x1x2=
⇒|x1-x2|=
=
…13分
将y=kx+b代人椭圆C2方程，得：（3+4k2）x2+8kbx+4b2-36=0
∴x3+x4=-
，x3x4=
⇒|x3-x4|=
…14分
∴x1+x2=x3+x4，可得线段PS、QR中点相同，∴|PQ|=|RS|
由
+
=2
⇒
=
，∴|PS|=3|QR|，可得：|x3-x4|=3|x1-x2|
∴
=3×
，
∴12k2+9=4b2（满足（*）式）．
故：动点E（k，b）的轨迹方程为
-
=1．…16分．
| x2 |
| a2 |
| y2 |
| b2 |
∴直线AB方程为：
| x |
| -a |
| y |
| b |
∴F1（-1，0）到直线AB距离为d=
| |b-ab| | ||
|
| ||
| 7 |
∴a2+b2=7（a-1）2…2分
又b2=a2-1，解得：a=2，b=
| 3 |
故：椭圆C1方程为：
| x2 |
| 4 |
| y2 |
| 3 |
（2）当直线l与x轴重合时，|PQ|=2，而|PR|•|PS|=1×5=5，∴|PQ|2≠|PR|•|PS|
若存在直线l，使|PQ|是|PR|、|PS|的等比中项，
则可设直线l方程为：x=my+3…5分
代人椭圆C1的方程，得：3（my+3）2+4y2=12，即：（3m2+4）y2+18my+15=0
∴△=（18m）2-4×15（3m2+4）=48（3m2-5）
记R（x1，y1），S（x2，y2），Q（x0，y0），
∴y1y2=
| 15 |
| 3m2+4 |
| 2 |
| m |
∵|PQ|2=|PR|•|PS|，即
| |PR| |
| |PQ| |
| |PQ| |
| |PS| |
| y1 |
| y0 |
| y0 |
| y2 |
∴y1y2=
| y | 2 0 |
∴
| 15 |
| 3m2+4 |
| 4 |
| m2 |
| 16 |
| 3 |
∴m=±
4
| ||
| 3 |
故存在直线l，使|PQ|是|PR|、|PS|的等比中项，其方程为x=±
4
| ||
| 3 |
| ||
| 4 |
（3）椭圆C1的3倍相似椭圆C2的方程为：
| x2 |
| 12 |
| y2 |
| 9 |
设Q、R、P、S各点坐标依次为（x1，y1）、（x2，y2）、（x3，y3）、（x4，y4）
将y=kx+b代人椭圆C1方程，得：（3+4k2）x2+8kbx+4b2-12=0
∴△1=(8kb)2-4(3+4k2)(4b2-12)=48(4k2+3-b2)＞0（*）
此时：x1+x2=-
| 8kb |
| 3+4k2 |
| 4b2-12 |
| 3+4k2 |
| (x1+x2)2-4x1x2 |
4
| ||
| 3+4k2 |
将y=kx+b代人椭圆C2方程，得：（3+4k2）x2+8kbx+4b2-36=0
∴x3+x4=-
| 8kb |
| 3+4k2 |
| 4b2-36 |
| 3+4k2 |
4
| ||
| 3+4k2 |
∴x1+x2=x3+x4，可得线段PS、QR中点相同，∴|PQ|=|RS|
由
| PS |
| RS |
| QS |
| PQ |
| QR |
∴
4
| ||
| 3+4k2 |
4
| ||
| 3+4k2 |
∴12k2+9=4b2（满足（*）式）．
故：动点E（k，b）的轨迹方程为
| 4b2 |
| 9 |
| 4k2 |
| 3 |
点评：本题考查椭圆方程，考查直线与椭圆的位置关系，考查向量知识的运用，考查韦达定理，考查学生分析解决问题的能力，有难度．
练习册系列答案
相关题目
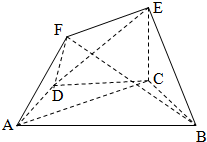如图，在多面体ABCDEF中，底面ABCD是梯形，且满足AD=DC=CB=
（文）已知中心在原点O，左焦点为F1（-1，0）的椭圆C的左顶点为A，上顶点为B，F1到直线AB的距离为
已知数列{an}中，a1=1，an+1=2an+n-1，若利用如图所示的程序框图进行运算，则输出n的值为