Question

（文）已知中心在原点O，左焦点为F₁（-1，0）的椭圆C的左顶点为A，上顶点为B，F₁到直线AB的距离为

7

7

|OB|．
（1）求椭圆C的方程；
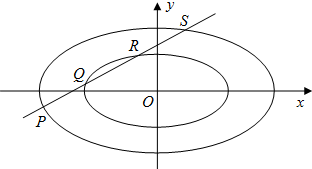
（2）过P（3，0）的直线l交椭圆C于R、S两点，交直线x=1于Q点，若|PQ|是|PR|、|PS|的等比中项，求直线l的方程；
（3）圆D以椭圆C的两焦点为直径，圆D的任意一条切线m交椭圆C于两点M、N，试求弦长|MN|的取值范围．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）确定直线AB方程，利用F₁到直线AB的距离为

7

7

|OB|，结合b²=a²-1，求出椭圆的几何量，即可求椭圆C₁的方程；
（2）分类讨论，设直线l方程为：x=my+3，代人椭圆C₁的方程，利用|PQ|是|PR|、|PS|的等比中项，结合韦达定理，即可求出直线l的方程；
（3）确定圆D的方程，分类讨论，设方程y=kx+b代人椭圆C方程，利用韦达定理，结合弦长公式，即可求弦长|MN|的取值范围．

解答： 解：（1）设椭圆C方程为：

x2

a2

+

y2

b2

=1（a＞b＞0）
∴直线AB方程为：

x

-a

+

y

b

=1…1分
∴F₁（-1，0）到直线AB距离为d=

|b-ab|

a2+b2

=

7

7

b，
∴a²+b²=7（a-1）²…2分
又b²=a²-1，解得：a=2，b=

3

…3分
故：椭圆C方程为：

x2

4

+

y2

3

=1．…4分
（2）当直线l与x轴重合时，|PQ|=2，而|PR|•|PS|=1×5=5，∴|PQ|²≠|PR|•|PS|
故可设直线l方程为：x=my+3，…5分
代人椭圆C的方程，得：3（my+3）²+4y²=12，即：（3m²+4）y²+18my+15=0
∴△=（18m）²-4×15（3m²+4）=48（3m²-5）
记R（x₁，y₁），S（x₂，y₂），Q（x₀，y₀），
∴y1y2=

15

3m2+4

，y0=-

2

m

…7分
∵|PQ|²=|PR|•|PS|，即

|PR|

|PQ|

=

|PQ|

|PS|

⇒

y1

y0

=

y0

y2

，∴y1y2=

y

2 0

∴

15

3m2+4

=

4

m2

，解得：m2=

16

3

，符合△＞0，
∴m=±

4 3

3

…9分
故直线l的方程为x=±

4 3

3

y+3，即：y=±

3

4

(x-3)…10分
（3）椭圆C的两焦点为F₁（-1，0）、F₂（1，0），∴圆D的方程为：x²+y²=1
①若切线m垂直于x轴，则其方程为：x=±1，易求得|MN|=3…11分
②若切线m不垂直于x轴，可设其方程为：y=kx+b
∴

|b|

k2+1

=1，
∴b²=k²+1
将y=kx+b代人椭圆C方程，得：（3+4k²）x²+8kbx+4b²-12=0
∴△=（8kb）²-4（3+4k²）（4b²-12）=48（4k²+3-b²）=48（3k²+2）＞0（*）…13分
记M、N两点的坐标分别为（x₃，y₃）、（x₄，y₄）
此时：x3+x4=-

8kb

3+4k2

，x3x4=

4b2-12

3+4k2

⇒|x3-x4|=

4 3(4k2+3-b2)

3+4k2

∴|MN|=

1+k2

×

4 3(4k2+3-b2)

3+4k2

=

1+k2

×

4 3(3k2+2)

3+4k2

…15分
令3+4k²=t，所以t≥3，k2=

t-3

4

∴|MN|=f(t)=

t+1 4

×

4 3× 3t-1 4

t

=

3(t+1)(3t-1)

t

=

3(- 1 t2 + 2 t +3)

，
t≥3⇒0＜

1

t

≤

1

3

⇒3＜-

1

t2

+

2

t

+3≤

32

9

⇒3＜|MN|≤

4 6

3

…17分
综合①②，得：弦长|MN|的取值范围为[3，

4 6

3

]．…18分．

点评：本题考查椭圆方程，考查直线与椭圆的位置关系，考查韦达定理，考查弦长公式，考查学生分析解决问题的能力，属于中档题．