题目内容
已知函数f(x)=ln(x+1)-x.
(1)求函数f(x)在x=-
处的切线方程;
(2)当x1>x2>-1时,求证:f(
)>
[f(x1)+f(x2)];
(3)若k∈R,且xf(x-1)+x2-k(x-1)>0对任意x>1恒成立,求k的最大值.
(1)求函数f(x)在x=-
| 1 |
| 2 |
(2)当x1>x2>-1时,求证:f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
(3)若k∈R,且xf(x-1)+x2-k(x-1)>0对任意x>1恒成立,求k的最大值.
考点:利用导数研究曲线上某点切线方程,函数恒成立问题
专题:综合题,导数的综合应用
分析:(1)求导函数,求出切线的斜率,切点坐标,即可求函数f(x)在x=-
处的切线方程;
(2)利用作差法,结合基本不等式,即可证明结论;
(3)令g(x)=
=
(x>1)⇒g′(x)=
(x>1),再构造函数h(x)=x-lnx-2(x>1)⇒h′(x)=
>0⇒h(x)在(1,+∞)上单调递增,利用k<[g(x)]min,即可求k的最大值.
| 1 |
| 2 |
(2)利用作差法,结合基本不等式,即可证明结论;
(3)令g(x)=
xf
| ||||
| x-1 |
| xlnx+x |
| x-1 |
| x-lnx-2 |
| (x-1)2 |
| x-1 |
| x |
解答:
(1)解:f(x)=ln(x+1)-x⇒f′(x)=
-1=
∴故切线斜率k=
|x=-
=1,f
=
-ln2
∴切线方程:y-(
-ln2)=x+
⇒x-y+1-ln2=0.
(2)证明:∵f(x)=ln(x+1)-x,
∴f(
)-
[f(x1)+f(x2)]=ln(
+1)-
-
[ln(x1+1)-x1+ln(x2+1)-x2]
=ln
-ln
,
∵x1>x2>-1,
∴
>
,
∴ln
-ln
>0,
∴f(
)>
[f(x1)+f(x2)]
(3)解:令g(x)=
=
(x>1)⇒g′(x)=
(x>1)
令h(x)=x-lnx-2(x>1)⇒h′(x)=
>0⇒h(x)在(1,+∞)上单调递增.
∵h(3)=1-ln3<0,h(4)=2-ln4>0,
∴h(x)存在唯一零点x0∈(3,4),即x0-lnx0-2=0.
当x∈(1,x0)时,h(x)<h(x0)=0⇒g′(x)<0;
当x∈(x0,+∞)时,h(x)>h(x0)=0⇒g′(x)>0;
∴g(x)在x∈(1,x0)时单调递减;在x∈(x0,+∞)时,单调递增;
∴[g(x)min]=g(x0)=
=
=x0
由题意k<[g(x)]min=x0,
∵k∈Z,∴k的最大值是3.
| 1 |
| x+1 |
| -x |
| x+1 |
∴故切线斜率k=
| -x |
| x+1 |
| 1 |
| 2 |
|
| 1 |
| 2 |
∴切线方程:y-(
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明:∵f(x)=ln(x+1)-x,
∴f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
=ln
| x1+x2+2 |
| 2 |
| (x1+1)(x2+1) |
∵x1>x2>-1,
∴
| x1+x2+2 |
| 2 |
| (x1+1)(x2+1) |
∴ln
| x1+x2+2 |
| 2 |
| (x1+1)(x2+1) |
∴f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
(3)解:令g(x)=
xf
| ||||
| x-1 |
| xlnx+x |
| x-1 |
| x-lnx-2 |
| (x-1)2 |
令h(x)=x-lnx-2(x>1)⇒h′(x)=
| x-1 |
| x |
∵h(3)=1-ln3<0,h(4)=2-ln4>0,
∴h(x)存在唯一零点x0∈(3,4),即x0-lnx0-2=0.
当x∈(1,x0)时,h(x)<h(x0)=0⇒g′(x)<0;
当x∈(x0,+∞)时,h(x)>h(x0)=0⇒g′(x)>0;
∴g(x)在x∈(1,x0)时单调递减;在x∈(x0,+∞)时,单调递增;
∴[g(x)min]=g(x0)=
| x0(lnx0+1) |
| x0-1 |
| x0(x0-1) |
| x0-1 |
由题意k<[g(x)]min=x0,
∵k∈Z,∴k的最大值是3.
点评:本题考查导数知识的综合运用,考查切线方程,考查函数的单调性与最值,考查学生分析解决问题的能力,正确构造函数是关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
执行如图所示的程序框图,若输入n的值为7,则输出的s的值为( )


| A、22 | B、16 | C、15 | D、11 |
若函数f(x)(x∈R)是奇函数,函数g(x)(x∈R)是偶函数,则一定成立的是( )
| A、函数f[g(x)]是奇函数 |
| B、函数g[f(x)]是奇函数 |
| C、函数f[f(x)]是奇函数 |
| D、函数g[g(x)]是奇函数 |
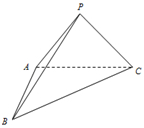 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=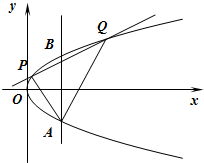 如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=
如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=