题目内容
6男4女站成一排，求满足下列条件的排法共有多少种？
（1）男生甲、乙、丙必须相邻，有多少种排法？
（2）任何2名女生都不相邻有多少种排法？
（3）男甲不在首位，男乙不在末位，有多少种排法？
（1）男生甲、乙、丙必须相邻，有多少种排法？
（2）任何2名女生都不相邻有多少种排法？
（3）男甲不在首位，男乙不在末位，有多少种排法？
考点：排列、组合的实际应用
专题：应用题,排列组合
分析：（1）男生甲、乙、丙必须相邻，利用捆绑法，可得结论；
（2）任何2名女生都不相邻，利用插空法；
（3）利用间接法求解，可得
-2
+
种排法．
（2）任何2名女生都不相邻，利用插空法；
（3）利用间接法求解，可得
| A | 10 10 |
| A | 9 9 |
| A | 8 8 |
解答：
解：（1）男生甲、乙、丙必须相邻，利用捆绑法，可得
=241920种排法；
（2）任何2名女生都不相邻，利用插空法，有
=604800种排法；
（3）利用间接法求解，可得
-2
+
=73
=2943360种排法．
| A | 8 8 |
| A | 3 3 |
（2）任何2名女生都不相邻，利用插空法，有
| A | 6 6 |
| A | 4 7 |
（3）利用间接法求解，可得
| A | 10 10 |
| A | 9 9 |
| A | 8 8 |
| A | 8 8 |
点评：本题考查排列知识的运用，考查捆绑法，插空法，间接法的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知数列{an}是等比数列，且an＞0，若bn=log2an，则（ ）
| A、{bn}一定是递增的等差数列 |
| B、{bn}不可能是等比数列 |
| C、{2b2n-1+1}是等差数列 |
| D、{3bn}不是等比数列 |
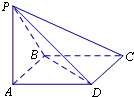如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PB⊥BC，PD⊥DC，且
如图，PA，PB是圆O的两条切线，A，B是切点，C是劣弧AB（不包括端点）上一点，直线PC交圆O于另一点D，Q在弦CD上，且∠DAQ=∠PBC．求证：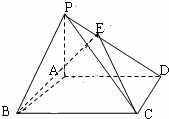
（理科）已知如图，四边形ABCD是矩形，PA⊥面ABCD，其中AB=3，PA=4．若在PD上存在一点E，使得BE⊥CE．
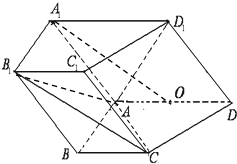如图，在四棱柱ABCD-A1B1C1D1中，侧面ADD1A1⊥底面ABCD，D1A=D1D=