题目内容
已知向量
=(sin(2x+
),sinx),
=(1,sinx),f(x)=
•
-
.
(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,a=2
,f(
)=
,若
sin(A+C)=2cosC,求b的大小.
| m |
| π |
| 6 |
| n |
| m |
| n |
| 1 |
| 2 |
(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,a=2
| 3 |
| A |
| 2 |
| 1 |
| 2 |
| 3 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算,正弦定理
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)利用向量的数量积公式,结合辅助角公式化简函数,再利用正弦函数的单调性,结合函数的定义域,即可得到结论;
(Ⅱ)由f(
)=
,可得A,利用两角和与差的三角函数以及正弦定理结合
sin(A+C)=2cosC,即可求边b的长.
(Ⅱ)由f(
| A |
| 2 |
| 1 |
| 2 |
| 3 |
解答:
解:(Ⅰ)f(x)=sin(2x+
)+sin2x-
=
sin2x+
cos2x+
-
=
sin2x…(4分)
所以f(x)递减区间是[kπ+
,kπ+
],k∈Z.…(5分)
(Ⅱ)由f(
)=
和f(x)=
sin2x得:sinA=
…(6分)
若cosA=
,而sin(A+C)=
cosC+
sinC
又
sin(A+C)=2cosC,所以cosC=
sinC
∵0<C<π,所以cosC=
若cosA=-
,同理可得:cosC=-
,显然不符合题意,舍去.…(9分)
∴sinB=sin(A+C)=
cosC=
…(10分)
由正弦定理得:b=
=4
…(12分)
| π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
所以f(x)递减区间是[kπ+
| π |
| 4 |
| 3π |
| 4 |
(Ⅱ)由f(
| A |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
若cosA=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
又
| 3 |
| 2 |
∵0<C<π,所以cosC=
| ||
| 3 |
若cosA=-
| ||
| 3 |
| ||
| 3 |
∴sinB=sin(A+C)=
| 2 | ||
|
2
| ||
| 3 |
由正弦定理得:b=
| asinB |
| sinA |
| 2 |
点评:本题考查向量知识的运用,考查三角函数的化简与三角函数的性质,考查正弦定理以及两角和与差的三角函数的运用,正确化简函数是关键.

练习册系列答案
相关题目
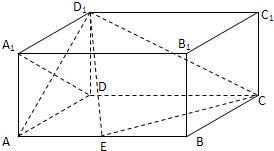 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.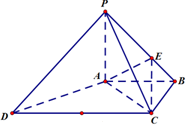 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC= 已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.
已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.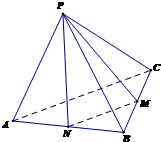 (文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示).
(文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示).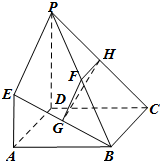 如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点. 如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2.