题目内容
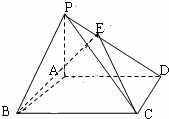 (理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.
(理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.(Ⅰ)求线段AD长度的取值范围;
(Ⅱ)若满足条件的E点有且只有一个,求二面角E-BC-A的正切值.
考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(Ⅰ)过点E作AD的垂线,垂足为F,连结BF,过点F作AB的平行线,交BC于G,连结EG,令EF=x,AD=a,利用勾股定理、根的判别式等知识点能线段AD长度的取值范围.
(Ⅱ)当a=4
时,方程4x2-12x+9=0有且仅有一个实根,由此能推导出存在唯一的点E.并能求出二面角E-BC-A的正切值.
(Ⅱ)当a=4
| 3 |
解答:
(理科)(Ⅰ)解:如图,过点E作AD的垂线,垂足为F,连结BF,
过点F作AB的平行线,交BC于G,连结EG,
令EF=x,AD=a,
∵PA⊥面ABCD,∴EF∥PA,
∴DF=
•AD=
,AF=(1-
)a,
∴BE2=BF2+EF2=AB2+AF2+EF2=9+(1-
)2a2+x2.
∵BE⊥CE,∴BC2=BE2+CE2.
∵BC=a,CE2=EF2+FC2=EF2+FD2+CD2=x2+
a2x2+9,
∴a2=18+(1+
-
)a2+2x2,
(
+2)x2-
x+18=0①.
由△≥0,得a4-36a2-576≥0,解得a≥4
.
∴线段AD长度的取值范围是[4
,+∞).…(5分)
(Ⅱ)由(Ⅰ)知,当a=4
时,
方程①即4x2-12x+9=0,△=0.
方程①有且仅有一个实根,
∴存在唯一的点E.
∵EF⊥面ABCD,BC⊥FG,BC⊥EG,
∴∠EGF是二面角E-BC-F的平面角,
tan∠EGF=
=
=
.
∴二面角E-BC-A的正切值为
.…(10分)
过点F作AB的平行线,交BC于G,连结EG,
令EF=x,AD=a,
∵PA⊥面ABCD,∴EF∥PA,
∴DF=
| EF |
| PA |
| ax |
| 4 |
| x |
| 4 |
∴BE2=BF2+EF2=AB2+AF2+EF2=9+(1-
| x |
| 4 |

∵BE⊥CE,∴BC2=BE2+CE2.
∵BC=a,CE2=EF2+FC2=EF2+FD2+CD2=x2+
| 1 |
| 16 |
∴a2=18+(1+
| x2 |
| 8 |
| x |
| 2 |
(
| a2 |
| 8 |
| a2 |
| 2 |
由△≥0,得a4-36a2-576≥0,解得a≥4
| 3 |
∴线段AD长度的取值范围是[4
| 3 |
(Ⅱ)由(Ⅰ)知,当a=4
| 3 |
方程①即4x2-12x+9=0,△=0.
方程①有且仅有一个实根,
∴存在唯一的点E.
∵EF⊥面ABCD,BC⊥FG,BC⊥EG,
∴∠EGF是二面角E-BC-F的平面角,
tan∠EGF=
| EF |
| GF |
| ||
| 3 |
| 1 |
| 2 |
∴二面角E-BC-A的正切值为
| 1 |
| 2 |
点评:本题考查线段长度取值范围的求法,考查二面角的正切值的求法,解题时要认真审题,注意合理地化空间问题为平面问题.

练习册系列答案
相关题目
 把边长为
把边长为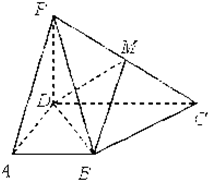 如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD,AD=CD=2AB=2,∠DAB=60°,PD⊥平面ABCD,M为PC的中点
如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD,AD=CD=2AB=2,∠DAB=60°,PD⊥平面ABCD,M为PC的中点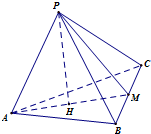 (理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示).
(理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示).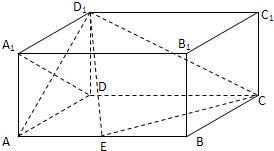 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.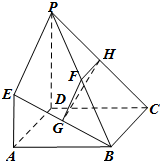 如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.