题目内容
如图，PA，PB是圆O的两条切线，A，B是切点，C是劣弧AB（不包括端点）上一点，直线PC交圆O于另一点D，Q在弦CD上，且∠DAQ=∠PBC．求证：（1）
| BD |
| AD |
| BC |
| AC |
（2）△ADQ∽△DBQ．
考点：相似三角形的性质,相似三角形的判定
专题：立体几何
分析：（Ⅰ）连接AB．利用△PBC∽△PDB，△PAC∽△PDA及PA=PB即可证明；
（II）利用△ABC∽△ADQ，及△ADQ∽△BDQ．即可得出．
（II）利用△ABC∽△ADQ，及△ADQ∽△BDQ．即可得出．
解答：
证明：
（Ⅰ）连接AB．
∵△PBC∽△PDB，
∴
=
．
同理
=
．
又∵PA=PB，
∴
=
，即
=
．
（Ⅱ）∵∠BAC=∠PBC=∠DAQ，∠ABC=∠ADQ，
∴△ABC∽△ADQ，即
=
．
故
=
．
又∵∠DAQ=∠PBC=∠BDQ，
∴△ADQ∽△BDQ．
（Ⅰ）连接AB．∵△PBC∽△PDB，
∴
| BD |
| BC |
| PD |
| PB |
同理
| AD |
| AC |
| PD |
| PA |
又∵PA=PB，
∴
| BD |
| BC |
| AD |
| AC |
| BD |
| AD |
| BC |
| AC |
（Ⅱ）∵∠BAC=∠PBC=∠DAQ，∠ABC=∠ADQ，
∴△ABC∽△ADQ，即
| BC |
| AC |
| DQ |
| AQ |
故
| BD |
| AD |
| DQ |
| AQ |
又∵∠DAQ=∠PBC=∠BDQ，
∴△ADQ∽△BDQ．
点评：本题考查了圆的切线长定理、切割线定理、相似三角形的判定与性质定理等基础知识与基本技能方法，属于基础题．
练习册系列答案
相关题目
如图，四面体ABCD中，点A在平面BCD上的射影O在BD上，点M、N分别是BC、BD的中点，AM与平面BCD成45°角，BC⊥CD，∠BDC=30°，BC=2，BO=1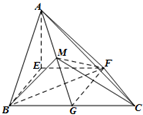
在直角梯形EFCB中，EF∥BC，EF=BE=
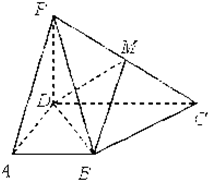如图，四棱锥P-ABCD中，底面ABCD为梯形，AB∥CD，AD=CD=2AB=2，∠DAB=60°，PD⊥平面ABCD，M为PC的中点
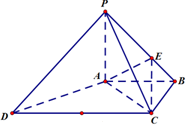如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为梯形，AB∥DC，∠ABC=90°，且PA=AB=BC=