题目内容
(1)已知不等式2x-1>m(x2-1)对任意m∈[-2,2]恒成立,求x的取值范围;
(2)是否存在m使得不等式2x-1>m(x2-1)对任意x∈[-2,2]恒成立.若存在,试求出m的取值范围;若不存在,试说明理由.
(2)是否存在m使得不等式2x-1>m(x2-1)对任意x∈[-2,2]恒成立.若存在,试求出m的取值范围;若不存在,试说明理由.
考点:函数恒成立问题
专题:函数思想,转化思想
分析:(1)不等式对任意m恒成立,可把m看作变量,x为常数,构造一次函数f(m),根据其单调性得到不等式组,再解出即可;
(2)先假设存在这样的m,然后根据x为变量,m为常数,构造函数f(x),对m=0,m>0,m<0讨论,注意对称轴与区间的关系,以及端点的函数值的符号,列出不等式组,解出它们,最后求并集,从而加以判断存在性.
(2)先假设存在这样的m,然后根据x为变量,m为常数,构造函数f(x),对m=0,m>0,m<0讨论,注意对称轴与区间的关系,以及端点的函数值的符号,列出不等式组,解出它们,最后求并集,从而加以判断存在性.
解答:
解:(1)不等式2x-1>m(x2-1)即2x-1-m(x2-1)>0,
令f(m)=2x-1-m(x2-1)=(1-x2)m+2x-1,m∈[-2,2],
要使原不等式对任意m∈[-2,2]恒成立,即f(m)>0对m∈[-2,2]都成立,
所以
即
即
,
所以
<x<
,
即x的取值范围是(
,
).
(2)假设存在m使得不等式2x-1>m(x2-1)对任意x∈[-2,2]恒成立,
令f(x)=2x-1-m(x2-1)=-mx2+2x+m-1,x∈[-2,2],
要使原不等式对任意x∈[-2,2]恒成立,即f(x)>0对x∈[-2,2]都成立,
当m=0时,f(x)=2x-1,在-2≤x≤
时,f(x)≤0,在
<x<2时,f(x)>0,
故不满足题意,舍去;
当m≠0时,f(x)只需满足下式:
或
或
,
即
或
或
,
解得结果为空集,故不存在m使得不等式2x-1>m(x2-1)对任意x∈[-2,2]恒成立.
令f(m)=2x-1-m(x2-1)=(1-x2)m+2x-1,m∈[-2,2],
要使原不等式对任意m∈[-2,2]恒成立,即f(m)>0对m∈[-2,2]都成立,
所以
|
|
|
所以
| ||
| 2 |
| ||
| 2 |
即x的取值范围是(
| ||
| 2 |
| ||
| 2 |
(2)假设存在m使得不等式2x-1>m(x2-1)对任意x∈[-2,2]恒成立,
令f(x)=2x-1-m(x2-1)=-mx2+2x+m-1,x∈[-2,2],
要使原不等式对任意x∈[-2,2]恒成立,即f(x)>0对x∈[-2,2]都成立,
当m=0时,f(x)=2x-1,在-2≤x≤
| 1 |
| 2 |
| 1 |
| 2 |
故不满足题意,舍去;
当m≠0时,f(x)只需满足下式:
|
|
|
即
|
|
|
解得结果为空集,故不存在m使得不等式2x-1>m(x2-1)对任意x∈[-2,2]恒成立.
点评:本题主要考查转化思想,即确定主元,同时考查构造函数思想,应用函数的性质解决,解题时还应对参数进行讨论,是一道很好的题目,属于中档题.

练习册系列答案
相关题目
在△ABC中,tanB=-2,tanC=
,则A等于( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
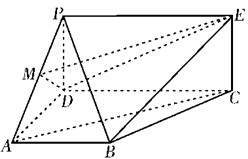 如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=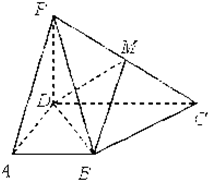 如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD,AD=CD=2AB=2,∠DAB=60°,PD⊥平面ABCD,M为PC的中点
如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD,AD=CD=2AB=2,∠DAB=60°,PD⊥平面ABCD,M为PC的中点
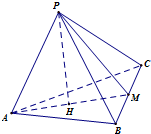 (理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示).
(理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示). 已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.
已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.