题目内容
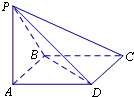 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且PC=
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且PC=| 3 |
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求二面角B-PD-C的余弦值;
(Ⅲ)棱PD上是否存在一点E,使直线EC与平面BCD所成的角是30°?若存在,求PE的长;若不存在,请说明理由.
考点:用空间向量求平面间的夹角,直线与平面平行的性质,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间向量及应用
分析:(Ⅰ)由已知条件推导出CD⊥PA,BC⊥PA,由此能够证明PA⊥平面ABCD.
(Ⅱ)连接AC,由(Ⅰ)和题设条件知PA⊥平面ABCD.分别以AD,AB,AP所在的直线分别为x,y,z轴,
建立空间直角坐标系,利用向量法能求出二面角B-PD-C的余弦值.
(Ⅲ)棱PD上存在点E满足条件,设
=λ
=(λ,0,-λ),λ∈[0,1].由平面BCD的一个法向量为
=(0,0,1).能求出棱PD上存在点E,使直线EC与平面BCD所成的角是30°,并能求出此时PE的长.
(Ⅱ)连接AC,由(Ⅰ)和题设条件知PA⊥平面ABCD.分别以AD,AB,AP所在的直线分别为x,y,z轴,
建立空间直角坐标系,利用向量法能求出二面角B-PD-C的余弦值.
(Ⅲ)棱PD上存在点E满足条件,设
| PE |
| PD |
| AP |
解答:
(本小题满分11分)
(Ⅰ)证明:在正方形ABCD中,CD⊥AD.
∵CD⊥PD,AD∩PD=D,∴CD⊥平面PAD.…(1分)
∵PA?平面PAD,∴CD⊥PA.…(2分)
同理,BC⊥PA.
∵BC∩CD=C,
∴PA⊥平面ABCD.…(3分)
(Ⅱ)解:连接AC,由(Ⅰ)知PA⊥平面ABCD.
∵AC?平面ABCD,PA⊥AC.…(4分)
∵PC=
,AC=
,∴PA=1.
 分别以AD,AB,AP所在的直线分别为x,y,z轴,
分别以AD,AB,AP所在的直线分别为x,y,z轴,
建立空间直角坐标系,如图所示.
由题意可得:B(0,1,0),D(1,0,0),C(1,1,0),P(0,0,1).
∴
=(0,1,0),
=(-1,0,1),
=(1,-1,0),
=(0,-1,1).
设平面PDC的一个法向量
=(x,y,z),
则
,∴
,
令x=1,得z=1,∴
=(1,0,1).
设平面PDB的一个法向量
=(x1,y1,z1),
则
,∴
,
∴
=(1,1,1). …(6分)
∴cos<
,
>=
=
.
∴二面角B-PD-C的余弦值为
.…(8分)
(Ⅲ)存在.理由如下:
若棱PD上存在点E满足条件,设
=λ
=(λ,0,-λ),λ∈[0,1].
∴
=
-
=(1,1,-1)-(λ,0,-λ)=(1-λ,1,λ-1).…(9分)
∵平面BCD的一个法向量为
=(0,0,1).
∴|cos<
,
>|=|
|=|
|.
令 |
|=sin30°=
,解得:λ=1±
.
经检验λ=1-
∈[0,1].
∴棱PD上存在点E,使直线EC与平面BCD所成的角是30°,
此时PE的长为
-1.…(11分)
(Ⅰ)证明:在正方形ABCD中,CD⊥AD.
∵CD⊥PD,AD∩PD=D,∴CD⊥平面PAD.…(1分)
∵PA?平面PAD,∴CD⊥PA.…(2分)
同理,BC⊥PA.
∵BC∩CD=C,
∴PA⊥平面ABCD.…(3分)
(Ⅱ)解:连接AC,由(Ⅰ)知PA⊥平面ABCD.
∵AC?平面ABCD,PA⊥AC.…(4分)
∵PC=
| 3 |
| 2 |
 分别以AD,AB,AP所在的直线分别为x,y,z轴,
分别以AD,AB,AP所在的直线分别为x,y,z轴,建立空间直角坐标系,如图所示.
由题意可得:B(0,1,0),D(1,0,0),C(1,1,0),P(0,0,1).
∴
| DC |
| DP |
| BD |
| BP |
设平面PDC的一个法向量
| n |
则
|
|
令x=1,得z=1,∴
| n |
设平面PDB的一个法向量
| m |
则
|
|
∴
| m |
∴cos<
| m |
| n |
| 1+0+1 | ||||
|
| ||
| 3 |
∴二面角B-PD-C的余弦值为
| ||
| 3 |
(Ⅲ)存在.理由如下:
若棱PD上存在点E满足条件,设
| PE |
| PD |
∴
| EC |
| PC |
| PE |
∵平面BCD的一个法向量为
| AP |
∴|cos<
| EC |
| AP |
| ||||
|
|
| λ-1 | ||
|
令 |
| λ-1 | ||
|
| 1 |
| 2 |
| ||
| 2 |
经检验λ=1-
| ||
| 2 |
∴棱PD上存在点E,使直线EC与平面BCD所成的角是30°,
此时PE的长为
| 2 |
点评:本题考查直线与平面垂直的证明,考查二面角余弦值的求法,考查满足条件的点是否存在的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为
如图是一个几何体的三视图,若它的体积为2,则a+b的最小值为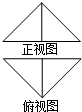 把边长为
把边长为 如图,四面体ABCD中,点A在平面BCD上的射影O在BD上,点M、N分别是BC、BD的中点,AM与平面BCD成45°角,BC⊥CD,∠BDC=30°,BC=2,BO=1
如图,四面体ABCD中,点A在平面BCD上的射影O在BD上,点M、N分别是BC、BD的中点,AM与平面BCD成45°角,BC⊥CD,∠BDC=30°,BC=2,BO=1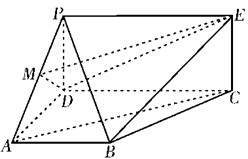 如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=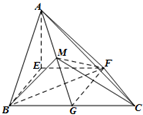 在直角梯形EFCB中,EF∥BC,EF=BE=
在直角梯形EFCB中,EF∥BC,EF=BE= 如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD,AD=CD=2AB=2,∠DAB=60°,PD⊥平面ABCD,M为PC的中点
如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD,AD=CD=2AB=2,∠DAB=60°,PD⊥平面ABCD,M为PC的中点 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.