题目内容
在不等式|x-1|+|x-4|≥3中,等号成立的充要条件是( )
| A、x≥4或x≤1 |
| B、1≤x≤4 |
| C、x=4或x=1 |
| D、x∈R |
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用,简易逻辑
分析:令|x-1|+|x-4|=3,讨论当x>4,当x<1时,当1≤x≤4时,等式成立的条件是否恒成立,即可得到.
解答:
解:令|x-1|+|x-4|=3
当x>4得x-1+x-4=3,即2x=8,则x>4不成立;
当x<1时,1-x+4-x=3,即有x=1不成立;
当1≤x≤4时,x-1+4-x=3,恒成立.
故|x-1|+|x-4|=3?1≤x≤4.
故选B.
当x>4得x-1+x-4=3,即2x=8,则x>4不成立;
当x<1时,1-x+4-x=3,即有x=1不成立;
当1≤x≤4时,x-1+4-x=3,恒成立.
故|x-1|+|x-4|=3?1≤x≤4.
故选B.
点评:本题考查绝对值不等式等号成立的条件,考查分类讨论的思想方法,考查运算能力,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
一个命题的结论是“自然数a,b,c中恰有一个是偶数”,用反证法证明该命题时,正确假设的是( )
| A、a,b,c都是奇数 |
| B、a,b,c都是偶数 |
| C、a,b,c都是奇数或a,b,c中至少两个是偶数 |
| D、a,b,c中至少两个是偶数 |
如图程序框图是古代一数学家的算法程序框图,它输出的结果S代表( )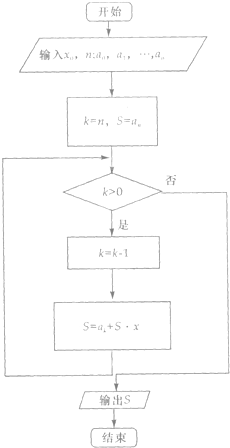

| A、一个数列的和 |
| B、一个n次多项式系数的和 |
| C、自变量取x.时,n次多项式函数的值 |
| D、自变量取x时,n个代数式的值 |
在△ABC中,AB=
,A=45°,B=75°,则BC=( )
| 3 |
A、
| ||
| B、2 | ||
C、3-
| ||
D、3+
|
设等差数列{an}的前n项和为Sn,已知S12>0,S13<0,则S1、S2、…、S12中值最大的为( )
| A、S6 |
| B、S7 |
| C、S6或S7 |
| D、不确定 |
下列程序框通常用来表示赋值、计算功能的是( )
A、. |
B、 |
C、. |
D、. |
函数f(x)=3sinx+5sin(x+60°)的最大值是( )
| A、8 | B、7 | C、6.5 | D、5.5 |
对于实数x,y满足命题p:x+y≠8,命题q:x≠2或y≠6,则命题p是命题q的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
an=
时,数列{an}的最小项是( )
n-
| ||
n-
|
| A、a1 |
| B、a44 |
| C、a45 |
| D、a50 |