题目内容
对于实数x，y满足命题p：x+y≠8，命题q：x≠2或y≠6，则命题p是命题q的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义以及逆否命题的等价性即可得到结论．
解答：
解：￢p：x+y=8，￢q：x=2且y=6，
当x=2且y=6时，x+y=8成立，
当x=1且y=7时满足x+y=8，但x=2且y=6不成立，
即￢q是￢p的充分不必要条件，
则根据逆否命题的等价性可知命题p是命题q的充分不必要条件，
故选：B
当x=2且y=6时，x+y=8成立，
当x=1且y=7时满足x+y=8，但x=2且y=6不成立，
即￢q是￢p的充分不必要条件，
则根据逆否命题的等价性可知命题p是命题q的充分不必要条件，
故选：B
点评：本题主要考查充分条件和必要条件的判断，根据逆否命题的等价性进行转化是解决本题的关键．否则不太容易判断．
练习册系列答案
精英口算卡系列答案
相关题目
与向量
=（-5，4）平行的向量是（ ）
| a |
| A、（-5k，4k） | ||||
B、（-
| ||||
| C、（-10，2） | ||||
| D、（5k，4k） |
在不等式|x-1|+|x-4|≥3中，等号成立的充要条件是（ ）
| A、x≥4或x≤1 |
| B、1≤x≤4 |
| C、x=4或x=1 |
| D、x∈R |
已知复数z=
，则z的共轭复数等于（ ）
| 1-i |
| 1+i |
| A、i | B、2i | C、-i | D、-2i |
k=5是直线l1：（k-3）x+（4-k）y+1=0与l2：2（k-3）x-2y+3=0平行的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
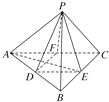
如图，在正四面体P-ABC中，D、E、F分别是AB、BC、CA的中点，下面四个结论不成立的是（ ）
| A、BC∥平面PDF |
| B、DF⊥平面PAE |
| C、平面PDF⊥平面PAE |
| D、平面PDE⊥平面ABC |
点通过矩阵M1=
和M2=
的变换效果相当于另一变换是（ ）
|
|
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|
若关于x的不等式|x-1|+|x+2|＜a的解集为空集，则实数a的取值范围是（ ）
| A、（-∞，3） |
| B、（-∞，3] |
| C、[3，+∞） |
| D、（3，+∞） |