题目内容
在数学拓展课上，老师定义了一种运算“*”：对于n∈N，满足以下运算性质：①2*2=1；②（2n+2）*2=（2n*2）+3．则1020*2的数值为（ ）
| A、1532 | B、1533 |
| C、1528 | D、1536 |
考点：进行简单的合情推理
专题：规律型
分析：根据：①2※2=1；②（2n+2）※2=（2n※2）+3，判断数列{（2n※2）}是等比数列，即可求得其通项公式，进而可求得1020※2的数值．
解答：
解：∵2※2=1，；（2n+2）※2=（2n※2）+3，
∴[2（n+1）※2]-（2n※2）=3
∴{ （2n※2）}是以1为首项，3为公差的等差数列，
∴（2n※2）=1+3（n-1）=3n-2
∴1020※2=3×510-2=1528．
故选C．
∴[2（n+1）※2]-（2n※2）=3
∴{ （2n※2）}是以1为首项，3为公差的等差数列，
∴（2n※2）=1+3（n-1）=3n-2
∴1020※2=3×510-2=1528．
故选C．
点评：考查对新定义的理解及等比数列的定义和通项公式的求法，旨在考查学生的观察分析和归纳能力，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在等差数列{an}中，a3+a7=2，则a2+a4+a6+a8=（ ）
| A、4 | B、2 | C、1 | D、0 |
已知M（-3，0），N（3，0），|PM|+|PN|=6，则动点P的轨迹是（ ）
| A、椭圆 | B、以M，N为端点的线段 |
| C、一条射线 | D、双曲线 |
下列函数中，在（0，+∞）上是减函数的是（ ）
A、y=
| |||||
| B、y=x2 | |||||
| C、y=2x | |||||
D、y=
|
设f（x）=
，则不等式f（x）≥2的解集为（ ）
|
| A、（-∞，1]∪[3，+∞） |
| B、（-∞，-1]∪[2，+∞） |
| C、[3，+∞） |
| D、（-∞，-1] |
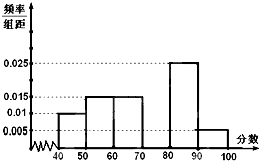某校从参加高一年级期中考试的学生中抽出60名学生，将其数学成绩（均为整数）分成六段[40，50），[50，60）…，[80，90），[90，100]，然后画出如图所示部分频率分布直方图．观察图形的信息，回答下列问题：