题目内容
已知A,B,C三点的坐标分别为A(3,0),B(0,3),C(cosα,sinα),α∈(
,
).
(Ⅰ)若|
|=|
|,求角α的值;
(Ⅱ)求y=
(3sinαcosα-
•
+1)的范围.
| π |
| 2 |
| 3π |
| 2 |
(Ⅰ)若|
| AC |
| BC |
(Ⅱ)求y=
| 1 |
| 3 |
| AC |
| BC |
考点:平面向量数量积的运算,正弦函数的定义域和值域
专题:综合题,平面向量及应用
分析:(Ⅰ)用坐标表示
、
,由|
|=|
|,求出角α的值;
(Ⅱ)由y=
(3sinαcosα-
•
+1)=sinα+cosα+sinαcosα,设sinα+cosα=t,求出t的取值范围,得sinαcosα=
,把函数化为y=f(t),求出y的取值范围即可.
| AC |
| BC |
| AC |
| BC |
(Ⅱ)由y=
| 1 |
| 3 |
| AC |
| BC |
| t2-1 |
| 2 |
解答:
解:(Ⅰ)∵
=(cosα-3,sinα),
=(cosα,sinα-3),
∴|
|=
=
,
|
|=
=
,
∵|
|=|
|,
∴sinα=cosα;
又α∈(
,
),∴α=
;
(Ⅱ)∵y=
(3sinαcosα-
•
+1)=sinα+cosα+sinαcosα,
设sinα+cosα=t,
∴t=
sin(α+
),且α∈(
,
),
∴α+
∈(
,
),
∴sin(α+
)∈[-1,
),
∴t∈[-
,1),
又sinαcosα=
,
∴y=t+
=
t2+t-
=
(t+1)2-1,
∴-1≤y<1;
∴函数y的取值范围是[-1,1).
| AC |
| BC |
∴|
| AC |
| (cosα-3)2+sin2α |
| 10-6cosα |
|
| BC |
| cos2α+(sinα-3)2 |
| 10-6sinα |
∵|
| AC |
| BC |
∴sinα=cosα;
又α∈(
| π |
| 2 |
| 3π |
| 2 |
| 5π |
| 4 |
(Ⅱ)∵y=
| 1 |
| 3 |
| AC |
| BC |
设sinα+cosα=t,
∴t=
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
∴α+
| π |
| 4 |
| 3π |
| 4 |
| 7π |
| 4 |
∴sin(α+
| π |
| 4 |
| ||
| 2 |
∴t∈[-
| 2 |
又sinαcosα=
| t2-1 |
| 2 |
∴y=t+
| t2-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴-1≤y<1;
∴函数y的取值范围是[-1,1).
点评:本题考查了平面向量的应用问题,解题时应结合三角函数的知识进行解答,是综合性题目.

练习册系列答案
相关题目
在数学拓展课上,老师定义了一种运算“*”:对于n∈N,满足以下运算性质:①2*2=1;②(2n+2)*2=(2n*2)+3.则1020*2的数值为( )
| A、1532 | B、1533 |
| C、1528 | D、1536 |
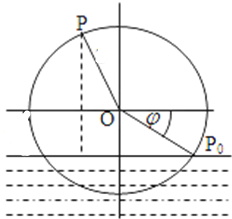 一半径为2
一半径为2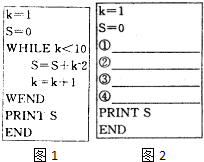 图1给出一个用“当型”循环语句编写的程序:
图1给出一个用“当型”循环语句编写的程序: