题目内容
在等差数列{an}中,a3+a7=2,则a2+a4+a6+a8=( )
| A、4 | B、2 | C、1 | D、0 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:利用等差数列的通项公式求解.
解答:
解:等差数列{an}中,
∵a3+a7=2,
∴a2+a4+a6+a8
=2(a3+a7)
=2×2=4.
故选:A.
∵a3+a7=2,
∴a2+a4+a6+a8
=2(a3+a7)
=2×2=4.
故选:A.
点评:本题考查等差数列若干项和的计算,是基础题,解题时要认真审题,注意等差数列的通项公式的合理运用.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=n2+
,则( )
| 2 |
| 3 |
| A、an=2n-1 | |||||||
| B、an=2n+1 | |||||||
C、an=
| |||||||
D、an=
|
与角-
终边相同的角是( )
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在数学拓展课上,老师定义了一种运算“*”:对于n∈N,满足以下运算性质:①2*2=1;②(2n+2)*2=(2n*2)+3.则1020*2的数值为( )
| A、1532 | B、1533 |
| C、1528 | D、1536 |
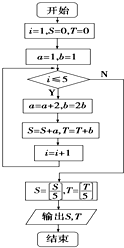 阅读程序框图设[x]表示取x的整数部分,如[5]=5,[2.7]=2,经过程序框图运行后输出结果为S,T,设z1=S-Ti,z2=1+i,z=z1•z2,则|z|=
阅读程序框图设[x]表示取x的整数部分,如[5]=5,[2.7]=2,经过程序框图运行后输出结果为S,T,设z1=S-Ti,z2=1+i,z=z1•z2,则|z|=