题目内容
5.以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线l的参数方程为$\left\{\begin{array}{l}x=2+tcosα\\ y=1+tsinα\end{array}\right.\;\;\;(t$为参数,0<α<π),曲线C的极坐标方程为ρsin2θ=4cosθ.(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)设点P的直角坐标为P(2,1),直线l与曲线C相交于A、B两点,并且$|PA|•|PB|=\frac{28}{3}$,求tanα的值.
分析 (I)对极坐标方程两边同乘ρ,得到直角坐标方程;
(II)将l的参数方程代入曲线C的普通方程,利用参数意义和根与系数的关系列出方程解出α.
解答 解:(I)∵ρsin2θ=4cosθ,∴ρ2sin2θ=4ρcosθ,
∴曲线C的直角坐标方程为y2=4x.
(II)将$\left\{\begin{array}{l}x=2+tcosα\\ y=1+tsinα\end{array}\right.$代入y2=4x,得sin2α•t2+(2sinα-4cosα)t-7=0,
所以$|{t_1}{t_2}|=\frac{7}{{{{sin}^2}α}}=\frac{28}{3}$,
所以${sin^2}α=\frac{3}{4}$,$α=\frac{π}{3}$或$\frac{2π}{3}$,即$tanα=\sqrt{3}$或$tanα=-\sqrt{3}$.
点评 本题考查了极坐标方程与直角坐标方程的转化,桉树方程的几何意义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.执行如图所示的程序框图,则输出的结果是( )
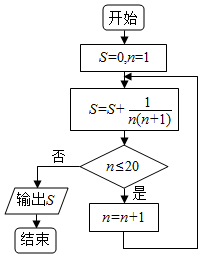

| A. | $\frac{22}{23}$ | B. | $\frac{21}{22}$ | C. | $\frac{20}{21}$ | D. | $\frac{19}{20}$ |
17.椭圆$\frac{{x}^{2}}{16}$+y2=1的长轴长为( )
| A. | 16 | B. | 2 | C. | 8 | D. | 4 |