Question

15．已知F₁，F₂是椭圆的两个焦点，满足MF₁⊥MF₂的点M总在椭圆内部，则椭圆离心率的取值范围是（0，$\frac{\sqrt{2}}{2}$）．

Answer 1

分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），由已知得M点的轨迹是以原点O为圆心，半焦距c为半径的圆，该圆内含于椭圆，由此能求出椭圆离心率的取值范围．

解答 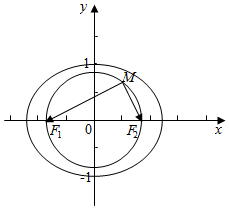解：设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），得F₁（-c，0），F₂（c，0）
∵MF₁⊥MF₂，
∴M点的轨迹是以原点O为圆心，半焦距c为半径的圆．
又∵M点总在椭圆内部，
∴该圆内含于椭圆，可得c＜b，
平方得c²＜b²，即c²＜a²-c²．
∴e²=$\frac{{c}^{2}}{{a}^{2}}$＜$\frac{1}{2}$，可得离心率e满足：0＜e＜$\frac{\sqrt{2}}{2}$．
∴椭圆离心率的取值范围是（0，$\frac{\sqrt{2}}{2}$）．
故答案为：（0，$\frac{\sqrt{2}}{2}$）．

点评 本题考查椭圆的离心率的取值范围的求法，是中档题，解题时要认真审题，注意椭圆、圆的性质的合理运用．