题目内容
20.设函数f(x)=lg(ax-bx),且f(1)=lg2,f(2)=lg12(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx-m的图象恒有两个交点.
分析 (1)由已知可得a-b=2,a2-b2=12,解得答案;
(2)当x∈[1,2]时,4x-2x∈[2,12],结合对数函数的图象和性质,可得答案;
(3)若函数g(x)=ax的图象与h(x)=bx-m的图象恒有两个交点,则4x-2x=-m有两个解,令t=2x,则t>0,则t2-t=-m有两个正解,进而得到答案.
解答 解:(1)∵f(x)=lg(ax-bx),且f(1)=lg2,f(2)=lg12,
∴a-b=2,a2-b2=12,
解得:a=4,b=2;
(2)由(1)得:函数f(x)=lg(4x-2x),
当x∈[1,2]时,4x-2x∈[2,12],
故当x=2时,函数f(x)取最大值lg12,
(3)若函数g(x)=ax的图象与h(x)=bx-m的图象恒有两个交点.
则4x-2x=-m有两个解,令t=2x,则t>0,
则t2-t=-m有两个正解;
则$\left\{\begin{array}{l}{1-4m>0}\\{m>0}\end{array}\right.$,
解得:m∈(0,$\frac{1}{4}$).
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
12.“$α=\frac{π}{2}$”是“cos2α=-1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
10.已知直线l和平面α,若l∥α,P∈α,则过点P且垂直于l的直线( )
| A. | 只有一条,不在平面α内 | B. | 只有一条,且在平面α内 | ||
| C. | 有无数条,一定在平面α内 | D. | 有无数条,不一定在平面α内 |
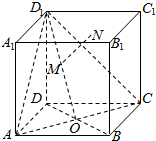 如图所示,正方体ABCD-A1B1C1D1的棱长为1,BD∩AC=O,M是线段D1O上的动点,过点M作平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为$\frac{\sqrt{6}}{2}$.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,BD∩AC=O,M是线段D1O上的动点,过点M作平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为$\frac{\sqrt{6}}{2}$.