题目内容
16．设f（x）是定义在实数集R上的函数，且满足f（x+2）=f（x+1）-f（x），如果$f（1）=lg\frac{3}{2}$，f（2）=lg15，则 f（0）=-1．分析 根据抽象函数关系令x=0，代入进行求解即可．
解答 解：∵f（x+2）=f（x+1）-f（x），
∴当x=0时，f（2）=f（1）-f（0），
即f（0）=f（1）-f（2），
∵$f（1）=lg\frac{3}{2}$，f（2）=lg15，
∴f（0）=f（1）-f（2）=lg$\frac{3}{2}$-lg15=lg（$\frac{3}{2}×\frac{1}{15}$）=lg$\frac{1}{10}$=-1，
故答案为：-1．
点评 本题主要考查函数值的计算，利用赋值法令x=0是解决本题的关键．比较基础．
练习册系列答案
阅读快车系列答案
相关题目
12．已知集合A={y|y=（$\frac{1}{2}$）x，x≥-1}，B={y|y=ex+1，x≤0}，则下列结论正确的是（ ）
| A． | A=B | B． | A∪B=R | C． | A∩（∁RB）=∅ | D． | B∩（∁RA）=∅ |
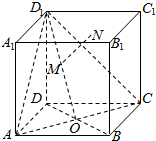如图所示，正方体ABCD-A1B1C1D1的棱长为1，BD∩AC=O，M是线段D1O上的动点，过点M作平面ACD1的垂线交平面A1B1C1D1于点N，则点N到点A距离的最小值为$\frac{\sqrt{6}}{2}$．
如图所示，扇形AOB，圆心角AOB的大小等于$\frac{π}{3}$，半径为2，在半径OA上有一动点C，过点C作平行于OB的直线交弧AB于点P．设∠COP=θ（θ∈（0，$\frac{π}{3}$）），则△POC周长与角θ的函数关系式f（θ）=$\frac{4\sqrt{3}}{3}$sin（$θ+\frac{π}{3}$）+2，θ∈（0，$\frac{π}{3}$）．