题目内容
15.求${(\frac{16}{81})^{-\frac{3}{4}}}+{log_3}\frac{5}{4}+{log_3}\frac{4}{5}+{π^0}$的值.分析 利用对数和指数幂的运算性质计算即可.
解答 解:${(\frac{16}{81})^{-\frac{3}{4}}}+{log_3}\frac{5}{4}+{log_3}\frac{4}{5}+{π^0}$=$(\frac{2}{3})^{4×(-\frac{3}{4})}$+log3$\frac{5}{4}×\frac{4}{5}$+1=$\frac{27}{8}$+0+1=$\frac{35}{8}$
点评 本题考查了指数和对数的运算性质,培养了学生的运算能力,属于基础题.

练习册系列答案
相关题目
10.已知直线l和平面α,若l∥α,P∈α,则过点P且垂直于l的直线( )
| A. | 只有一条,不在平面α内 | B. | 只有一条,且在平面α内 | ||
| C. | 有无数条,一定在平面α内 | D. | 有无数条,不一定在平面α内 |
7.圆C1:x2+y2-2x-6y+1=0与圆C2:x2+y2+4x+2y+1=0的公切线有且仅有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
5.已知函数f(x)=$\frac{x}{x+1}$+2x-mln(x+1)在(0,+∞)上是增函数,则实数m的取值范围为( )
| A. | (-∞,2$\sqrt{2}$] | B. | (-∞,2$\sqrt{2}$) | C. | (-∞,3) | D. | (-∞,3] |
 如图所示,扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ(θ∈(0,$\frac{π}{3}$)),则△POC周长与角θ的函数关系式f(θ)=$\frac{4\sqrt{3}}{3}$sin($θ+\frac{π}{3}$)+2,θ∈(0,$\frac{π}{3}$).
如图所示,扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ(θ∈(0,$\frac{π}{3}$)),则△POC周长与角θ的函数关系式f(θ)=$\frac{4\sqrt{3}}{3}$sin($θ+\frac{π}{3}$)+2,θ∈(0,$\frac{π}{3}$).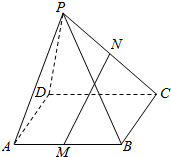 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,三角形ADP中AD=AP=5,PD=6,M、N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,三角形ADP中AD=AP=5,PD=6,M、N分别是AB,PC的中点.