题目内容
5．
已知a＞b，函数f（x）=（x-a）（x-b）的图象如图所示，则函数y=a（x-b）的图象可能为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 利用函数的图象特征，函数性质，逐一判断各个选项是否满足条件，从而得出结论．
解答 解：由于a＞b，结合函数f（x）=（x-a）（x-b）的图象，可得0＜b＜1＜a，
故函数y=a（x-b）为单调递增函数，函数的图象从左到右是上升的，故排除A、B；
再根据函数y=a（x-b）的图象经过定点（0，$\frac{1}{{a}^{b}}$），$\frac{1}{{a}^{b}}$＞0，故排除D，
故选：C．
点评 本题主要考查函数的图象特征，函数性质，属于中档题．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
6．已知数列{an}满足${a_1}，\frac{a_2}{a_1}，\frac{a_3}{a_2}，…\frac{a_n}{{{a_{n-1}}}}$是首项为1，公比为2的等比数列，则a101=（ ）
| A． | 2100 | B． | 24950 | C． | 25050 | D． | 25151 |
10．
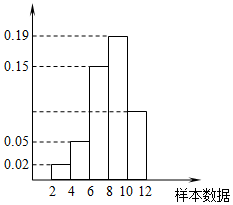有一个容量为300的样本，其频率分布直方图如图所示．根据样本的频率分布直方图估计，样本数据落在区间[10，12）内的频数为（ ）
有一个容量为300的样本，其频率分布直方图如图所示．根据样本的频率分布直方图估计，样本数据落在区间[10，12）内的频数为（ ）| A． | 27 | B． | 81 | C． | 54 | D． | 108 |
17．已知复数$z=\frac{m+i}{1+i}$（i为虚数单位）是纯虚数，则复数z的共轭复数的虚部是（ ）
| A． | -1 | B． | 1 | C． | -i | D． | i |
某中学随机抽取50名高二学生调查其每天运动的时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中运动的时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．