题目内容
17.已知复数$z=\frac{m+i}{1+i}$(i为虚数单位)是纯虚数,则复数z的共轭复数的虚部是( )| A. | -1 | B. | 1 | C. | -i | D. | i |
分析 由复数代数形式的乘除运算化简复数$z=\frac{m+i}{1+i}$,结合已知条件求出m的值,然后代入复数$z=\frac{m+i}{1+i}$化简即可求出z,则复数z的共轭复数的虚部可求.
解答 解:∵$z=\frac{m+i}{1+i}$=$\frac{(m+i)(1-i)}{(1+i)(1-i)}=\frac{1+m+(1-m)i}{2}$=$\frac{1+m}{2}+\frac{1-m}{2}i$是纯虚数,
∴$\left\{\begin{array}{l}{\frac{1+m}{2}=0}\\{\frac{1-m}{2}≠0}\end{array}\right.$,解得m=-1.
∴$z=\frac{-1+i}{1+i}=\frac{(-1+i)(1-i)}{(1+i)(1-i)}=\frac{2i}{2}=i$.
则$\overline{z}=-i$.
∴复数z的共轭复数的虚部是-1.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
2.如图所示,四边形ABCD中,$\overrightarrow{OA}+\overrightarrow{AB}-\overrightarrow{OB}$=( )


| A. | $\overrightarrow{CB}$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{BC}$ | D. | $\overrightarrow O$ |
 已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数y=a(x-b)的图象可能为( )
已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数y=a(x-b)的图象可能为( )



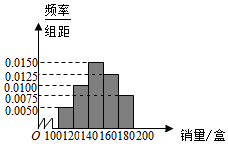 某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.