题目内容
已知抛物线D:y2=2px(p>0)的焦点为F,P是抛物线上一动点,Q是圆M:(x+1)2+(y-2)2=
上一动点,且|PF|+|PQ|最小值为
,求抛物线D的方程.
| 1 |
| 2 |
3
| ||
| 2 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:确定圆心坐标为M(-1,2),半径为
,将|PF|+|PQ|最小值为
,转化为|PF|+|PM|最小值为2
,即|FM|=2
,利用两点间距离公式,求出p,就可以求出抛物线D的方程.
| ||
| 2 |
3
| ||
| 2 |
| 2 |
| 2 |
解答:
解:圆M:(x+1)2+(y-2)2=
的圆心坐标为M(-1,2),半径为
,
∵|PF|+|PQ|最小值为
,Q是圆M:(x+1)2+(y-2)2=
上一动点,
∴当Q、P、F三点共线时,|QF|最小,M、Q、P、F四点共线时,|MF|最小为2
,
∴
=2
,
∴p=2,
∴抛物线D的方程是y2=4x.
| 1 |
| 2 |
| ||
| 2 |
∵|PF|+|PQ|最小值为
3
| ||
| 2 |
| 1 |
| 2 |
∴当Q、P、F三点共线时,|QF|最小,M、Q、P、F四点共线时,|MF|最小为2
| 2 |
∴
(
|
| 2 |
∴p=2,
∴抛物线D的方程是y2=4x.
点评:圆外点与圆上点的距离的最值,通常转化为点与圆心的距离问题.

练习册系列答案
相关题目
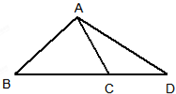 如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.
如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.