题目内容
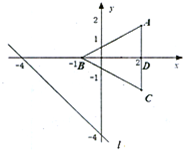 在等腰△ABC中,已知AB=AC,B(-1,0),边AC的中点为D(2,0).
在等腰△ABC中,已知AB=AC,B(-1,0),边AC的中点为D(2,0).(1)若点A(2,
| 3 |
(2)若点N在(1)中所求的圆M上,求线段BN在直线l:x+y+4=0上的投影EF长的最大值.
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆
分析:(1)由于BD⊥AC,D为AC的中点,M在BD上设圆M:(x-a)2+y2=r2,代入(-1,0),(2,
)解出a,r即可;
(2)根据题意可求得BE的方程,设出直线NF的方程,当EF取得最大值时,直线NF与圆(x-1)2+y2=4相切.利用点到直线的距离求得b,则直线NF的方程可得.进而根据EF长的最大值是点B到NF的距离,答案可得.
| 3 |
(2)根据题意可求得BE的方程,设出直线NF的方程,当EF取得最大值时,直线NF与圆(x-1)2+y2=4相切.利用点到直线的距离求得b,则直线NF的方程可得.进而根据EF长的最大值是点B到NF的距离,答案可得.
解答:
 解:(1)由于BD⊥AC,D为AC的中点,M在BD上
解:(1)由于BD⊥AC,D为AC的中点,M在BD上
设圆M:(x-a)2+y2=r2,
则代入(-1,0),(2,
)得,
解得a=1,r=2,
则△ABC外接圆M的方程为:(x-1)2+y2=4;
(2)由条件,BE⊥l,
易得BE:x-y+1=0.
设NF:x-y+b=0,
当EF取得最大值时,
直线NF与圆(x-1)2+y2=4相切.
设M(1,0),由
=2,得b=-1+2
(舍去)或b=-1-2
.
∴NF:x-y-1-2
=0.
∴EFmax等于点B到NF的距离
d=
=2+
.
 解:(1)由于BD⊥AC,D为AC的中点,M在BD上
解:(1)由于BD⊥AC,D为AC的中点,M在BD上设圆M:(x-a)2+y2=r2,
则代入(-1,0),(2,
| 3 |
|
则△ABC外接圆M的方程为:(x-1)2+y2=4;
(2)由条件,BE⊥l,
易得BE:x-y+1=0.
设NF:x-y+b=0,
当EF取得最大值时,
直线NF与圆(x-1)2+y2=4相切.
设M(1,0),由
| |1-0+b| | ||
|
| 2 |
| 2 |
∴NF:x-y-1-2
| 2 |
∴EFmax等于点B到NF的距离
d=
|-1-0-2
| ||
|
| 2 |
点评:本题主要考查了直线与圆的综合问题.考查了学生运用解析几何的知识解决问题的能力.

练习册系列答案
相关题目
 如图,已知PA是⊙O的切线,切点为A,点B是⊙O上一点,且PA=PB,判断PB与⊙O的位置关系,并说明理由.
如图,已知PA是⊙O的切线,切点为A,点B是⊙O上一点,且PA=PB,判断PB与⊙O的位置关系,并说明理由.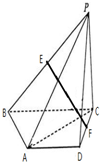 已知在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=
已知在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=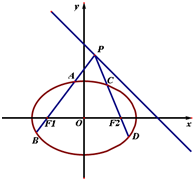 已知椭圆
已知椭圆