题目内容
已知|
|=2，|
|=4，向量
与
的夹角为60°，当（
+3
）⊥（k
-
）时，实数k的值是 ．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点：数量积判断两个平面向量的垂直关系,数量积表示两个向量的夹角
专题：平面向量及应用
分析：由已知得（
+3
）•（k
-
）=k
2+（3k-1）
•
-3
2=0，由此能求出实数k的值．
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
解答：
解：∵|
|=2，|
|=4，向量
与
的夹角为60°，
（
+3
）⊥（k
-
），
∴（
+3
）•（k
-
）
=k
2+（3k-1）
•
-3
2
=4k+（3k-1）×2×4×cos60°-3×16=0，
解得k=
．
故答案为：
．
| a |
| b |
| a |
| b |
（
| a |
| b |
| a |
| b |
∴（
| a |
| b |
| a |
| b |
=k
| a |
| a |
| b |
| b |
=4k+（3k-1）×2×4×cos60°-3×16=0，
解得k=
| 13 |
| 4 |
故答案为：
| 13 |
| 4 |
点评：本题考查实数值的求法，是基础题，解题时要认真审题，注意向量垂直的性质的合理运用．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
设i为虚数单位，则（1+i）4的值为（ ）
| A、4 | B、-4 | C、4i | D、-4i |
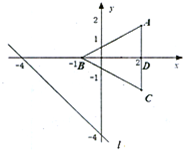在等腰△ABC中，已知AB=AC，B（-1，0），边AC的中点为D（2，0）．