题目内容
已知函数f(x)=e2x-1-2x.
(1)求函数f(x)的导数f'(x);
(2)证明:e2x-1>2x-2.
(1)求函数f(x)的导数f'(x);
(2)证明:e2x-1>2x-2.
考点:利用导数求闭区间上函数的最值,导数的运算
专题:导数的综合应用
分析:(1)利用导数的性质能求出f(x)=e2x-1-2x的导数.
(2)由f′(x)=2e2x-1-2=0 解得x=
,由导数性质得f(x)min=f(
)=0,由此能证明e2x-1>2x-2.
(2)由f′(x)=2e2x-1-2=0 解得x=
| 1 |
| 2 |
| 1 |
| 2 |
解答:
(1)解:∵f(x)=e2x-1-2x,
∴f′(x)=2e2x-1-2.(4分)
(2)证明:由f′(x)=2e2x-1-2=0 解得x=
,
x∈(-∞,
) 时,f'(x)<0;
x∈(
,+∞) 时,f'(x)>0.…(6分)
∴当x=
时,f(x)min=f(
)=0,
∴f(x)≥0>-2,即e2x-1-2x>-2,
∴e2x-1>2x-2.…(10分)
∴f′(x)=2e2x-1-2.(4分)
(2)证明:由f′(x)=2e2x-1-2=0 解得x=
| 1 |
| 2 |
x∈(-∞,
| 1 |
| 2 |
x∈(
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)≥0>-2,即e2x-1-2x>-2,
∴e2x-1>2x-2.…(10分)
点评:本题考查导数的求法,考查不等式的证明,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
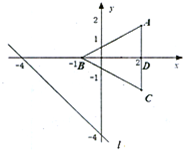 在等腰△ABC中,已知AB=AC,B(-1,0),边AC的中点为D(2,0).
在等腰△ABC中,已知AB=AC,B(-1,0),边AC的中点为D(2,0).