题目内容
如图，已知PA是⊙O的切线，切点为A，点B是⊙O上一点，且PA=PB，判断PB与⊙O的位置关系，并说明理由．考点：圆的切线的性质定理的证明
专题：证明题,立体几何
分析：连接OA，OB，OP，在△PAO和△PBO中，运用三边对应相等，则全等，得到对应角相等，即可得证．
解答：
解：PB与⊙O的位置关系：相切．
理由如下：连接OA，OB，OP，
在△PAO和△PBO中，
PA=PB，OA=OB，PO=PO，
则△PAO≌△PBO，
则∠PAO=∠PBO，
由于PA⊥OA，则PB⊥OB，
故PB与⊙O相切．
解：PB与⊙O的位置关系：相切．理由如下：连接OA，OB，OP，
在△PAO和△PBO中，
PA=PB，OA=OB，PO=PO，
则△PAO≌△PBO，
则∠PAO=∠PBO，
由于PA⊥OA，则PB⊥OB，
故PB与⊙O相切．
点评：本题考查圆的切线性质的运用，考查三角形的全等的判定和性质的运用，属于中档题．
练习册系列答案
相关题目
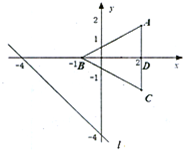在等腰△ABC中，已知AB=AC，B（-1，0），边AC的中点为D（2，0）．