题目内容
19.已知函数$f(x)=x-{e^{\frac{x}{a}}}$(a>0),且y=f(x)的图象在x=0处的切线l与曲y=ex相切,符合情况的切线( )| A. | 有0条 | B. | 有1条 | C. | 有2条 | D. | 有3条 |
分析 求出f(x)的导数,可得切线的斜率和切点,求得切线l的方程,再假设l与曲线y=ex相切,设切点为(x0,y0),即有e${\;}^{{x}_{0}}$=1-$\frac{1}{a}$=(1-$\frac{1}{a}$)x0-1,消去a得e${\;}^{{x}_{0}}$=e${\;}^{{x}_{0}}$•x0-1,设h(x)=exx-ex-1,求出导数和单调区间,可得h(x)在(0,+∞)有唯一解,由a>0,即可判断不存在.
解答 解:函数f(x)=x-e${\;}^{\frac{x}{a}}$的导数为f′(x)=1-$\frac{1}{a}$e${\;}^{\frac{x}{a}}$,a>0.
易知,曲线y=f(x)在x=0处的切线l的斜率为1-$\frac{1}{a}$,切点为(0,-1),
可得切线的方程为y=(1-$\frac{1}{a}$)x-1.
假设l与曲线y=ex相切,设切点为(x0,y0),
即有e${\;}^{{x}_{0}}$=1-$\frac{1}{a}$=(1-$\frac{1}{a}$)x0-1,
消去a得e${\;}^{{x}_{0}}$=e${\;}^{{x}_{0}}$•x0-1,设h(x)=exx-ex-1,
则h′(x)=exx,令h′(x)>0,则x>0,
所以h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
当x→-∞,h(x)→-1,x→+∞,h(x)→+∞,
所以h(x)在(0,+∞)有唯一解,则e${\;}^{{x}_{0}}$>1,
而a>0时,1-$\frac{1}{a}$<1,与e${\;}^{{x}_{0}}$>1矛盾,所以不存在.
故选:A.
点评 本题考查导数的运用:求切线的方程和单调区间,考查直线方程的运用和构造函数法,以及函数方程的转化思想的运用,属于中档题.

| A. | $\frac{2}{π}$ | B. | $\frac{π}{4}$ | C. | 2-$\frac{2}{π}$ | D. | 2-$\frac{π}{4}$ |
| A. | $[0,2+\sqrt{6}]$ | B. | $[2-\sqrt{6},2+\sqrt{6}]$ | C. | $[0,2+\sqrt{5}]$ | D. | $[2-\sqrt{5},2+\sqrt{5}]$ |
 函数φ(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若把函数φ(x)的图象纵坐标不变,横坐标扩大到原来的2倍,得到函数f(x).
函数φ(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若把函数φ(x)的图象纵坐标不变,横坐标扩大到原来的2倍,得到函数f(x).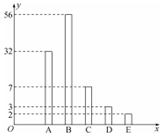 某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题: