题目内容
10.已知函数f(x)=|x-1|+|x-2|,记f(x)的最小值为k.(1)解不等式:f(x)≤x+1;
(2)是否存在正数a、b,同时满足:2a+b=k,$\frac{1}{a}$+$\frac{2}{b}$=4?若存在,求出a、b的值,若不存在,请说明理由.
分析 (1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(2)利用绝对值三角不等式求得k的值,若2a+b=k=1,$\frac{1}{a}$+$\frac{2}{b}$=4,可得2a2-a+4=0,由于△=-31<0,故此方程无解,故不存在正数a、b,同时满足:2a+b=k,$\frac{1}{a}$+$\frac{2}{b}$=4.
解答 解:(1)∵函数f(x)=|x-1|+|x-2|,不等式 f(x)≤x+1,即|x-1|+|x-2|≤x+1,
∴$\left\{\begin{array}{l}{x<1}\\{1-x+2-x≤x+1}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{1≤x≤2}\\{x-1+2-x≤x+1}\end{array}\right.$ ②,或 $\left\{\begin{array}{l}{x>2}\\{x-1+x-2≤x+1}\end{array}\right.$③.
解①求得$\frac{2}{3}$≤x<1,解②求得1≤x≤2,解③求得2<x≤4,
综上可得不等式的解集为{x|$\frac{2}{3}$≤x≤4}.
(2)∵f(x)=|x-1|+|x-2|≥|(x-1)-(x-2)|=1,当且仅当1≤x≤2时,取等号,故f(x)的最小值为k=1.
若2a+b=k=1,$\frac{1}{a}$+$\frac{2}{b}$=4,则 $\frac{2a+b}{ab}$=$\frac{1}{ab}$=4,即ab=a(1-2a)=a-2a2=4,
化简可得,2a2-a+4=0,由于△=-31<0,故此方程无解,
故不存在正数a、b,同时满足:2a+b=k,$\frac{1}{a}$+$\frac{2}{b}$=4.
点评 本题主要考查绝对值三角不等式的应用,解绝对值不等式,体现了分类讨论的数学思想,属于中档题.

 初中暑期衔接系列答案
初中暑期衔接系列答案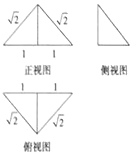 一个四面体的三视图如图所示,则该四面体的外接球的表面积为( )
一个四面体的三视图如图所示,则该四面体的外接球的表面积为( )| A. | $\frac{4π}{3}$ | B. | 4π | C. | $\frac{2π}{3}$ | D. | 2π |

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
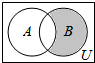
| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |