题目内容
19.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$({1,\frac{{\sqrt{2}}}{2}})$,其离心率为$\frac{{\sqrt{2}}}{2}$.(1)求椭圆C的方程;
(2)若直线y=x+m与C相交于A,B两点,∠AOB(O为坐标原点)为钝角,求实数m的取值范围.
分析 (1)由题意列关于a,b,c的方程组,求解方程组可得a,b的值,则椭圆方程可求;
(2)联立直线方程和椭圆方程,化为关于x的一元二次方程,由判别式大于0求得m的范围,再由根与系数的关系结合$\overrightarrow{AO}•\overrightarrow{BO}<0$进一步求得m的范围得答案.
解答 解:(1)由题意,$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=$\sqrt{2}$,b=1,c=1.
∴椭圆C的方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)联立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得3x2+4mx+2m2-2=0.
由△=16m2-12(2m2-2)>0,得m2<3.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=-\frac{4m}{3},{x}_{1}{x}_{2}=\frac{2{m}^{2}-2}{3}$,①
∵∠AOB为钝角,∴$\overrightarrow{AO}•\overrightarrow{BO}={x}_{1}{x}_{2}+{y}_{1}{y}_{2}<0$,
即$2{x}_{1}{x}_{2}+m({x}_{1}+{x}_{2})+{m}^{2}<0$,②
把①代入②得:$2×\frac{2{m}^{2}-2}{3}-\frac{4}{3}m×m+{m}^{2}<0$,
解得:$-\frac{2\sqrt{3}}{3}<m<\frac{2\sqrt{3}}{3}$.
∵A、B、O三点不共线,∴m≠0.
∴实数m的取值范围为($-\frac{2\sqrt{3}}{3},0$)∪(0,$\frac{2\sqrt{3}}{3}$).
点评 本题考查椭圆的简单性质,考查椭圆标准方程的求法,训练了平面向量在求解圆锥曲线问题中的应用,是中档题.

| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{28}{5}$ | D. | $\frac{12}{5}$ |
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(x≠±3) | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(x≠±5) | ||
| C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(x≠±3) | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(x≠±5) |
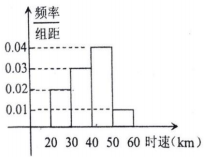 太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )
太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )| A. | 30辆 | B. | 35辆 | C. | 40辆 | D. | 50辆 |
| A. | $\frac{15}{4}$ | B. | $\frac{13}{4}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{5}$ |